Distribution of the product of $n$ uniform variables

Question

Let $(X_n)_{n\geq1}$ be iid following a uniform distribution on $]0,1[$. What is the distribution of $Z_n=\prod_{i=1}^n X_i$.

What I did is that I took the log of both sides and found myself with something like $\Pr(\sum_{i=1}^{n} \log(X_i)\leq \log(t)$) and can’t develop further. Can anybody please explain it to me?

Answer 1

We have $$ Z=\prod_{i=1}^n X_i, $$ where $X_i\sim\operatorname{Uniform}(0,1)$ are mutually independent standard uniform random variables. We want to find the distribution of $Z_n$.

---

First define $$ -W=-\log(Z_n)=\sum_{i=1}^n-\log X_i. $$ Then defining the transformation $Y_i=-\log X_i=g(X_i)\implies g^{-1}(Y_i)=e^{-Y_i}$ we have by change of variables the density of $Y_i$ given as $$ f_{Y_i}(y)=f_{X_i}(g^{-1}(y))e^{-y},\quad y\geq 0. $$ Upon inspection we conclude $Y_i\sim\operatorname{Exp}(1)$. It is well-known that sums of exponential random variables with equal parameters yields a gamma distributed variable, specifically $$ -W=\sum_{i=1}^n Y_i\sim\operatorname{Gamma}(n,1) $$ so that $$ f_W(w)=\frac{1}{\Gamma(n)}(-w)^{n-1}e^w,\quad w\leq 0. $$ To get the density for $Z_n$ we now recall $Z_n=g(W)=e^W\implies g^{-1}(Z_n)=\log Z_n$ to obtain $$ f_{Z_n}(z)=f_W(g^{-1}(z))\frac{1}{z}=\frac{1}{\Gamma(n)}(-\log z)^{n-1}e^{\log z}\frac{1}{z}. $$ Simplifying then gives the final result $$ f_{Z_n}(z)=\frac{1}{\Gamma(n)}(-\log z)^{n-1},\quad z\in(0,1). $$

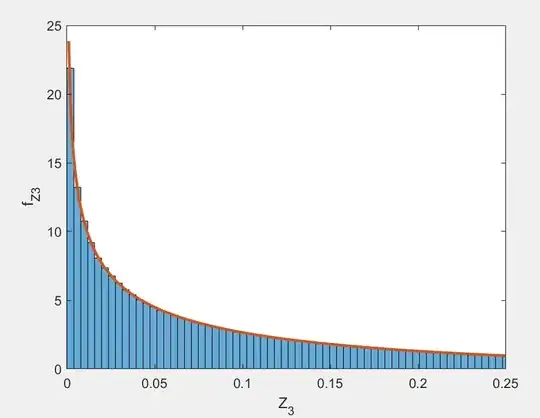
To see this result in action, here is some MATLAB code simulated $Z_3$ and plotting its histogram against the density $f_{Z_3}$

n=3;
Zn = prod(rand(n,1e6));
fZn = @(z) (-log(z)).^(n-1)/gamma(n);
ax = linspace(0.001,0.25,256);
figure
histogram(Zn,linspace(0,0.5,128),'Normalization','pdf')
hold on
plot(ax,fZn(ax),'LineWidth',2)
xlim([0,0.25])
ylabel(['f_{Z' num2str(n) '}'])
xlabel(['Z_' num2str(n)])

Here is the resulting plot: