2

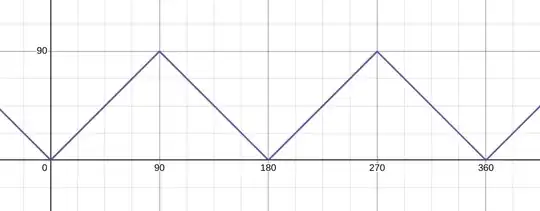
I am trying to short-cut the following with modulo, but it is not working for 90 and 270 degrees. What is the correct short-cut?

\begin{equation} \delta'= \begin{cases} \delta & \text{if } 0 \le \delta \le 90 \\\\ 180 - \delta & \text{if } 90 \lt \delta \le 180 \\\\ \delta - 180 & \text{if } 180 \lt \delta \le 270 \\\\ 360 - \delta & \text{if } 270 \lt \delta \le 360 \\\\ \end{cases} \end{equation}

Trying: \delta % 90

delta expected delta-prime calculated equal?
0 0 0 TRUE
30 30 30 TRUE
45 45 45 TRUE
60 60 60 TRUE
90 90 0 FALSE
105 75 75 TRUE
130 50 50 TRUE
150 30 30 TRUE
180 0 0 TRUE
200 20 20 TRUE
220 40 40 TRUE
230 50 50 TRUE
270 90 0 FALSE
280 80 80 TRUE
300 60 60 TRUE
320 40 40 TRUE
330 30 30 TRUE
350 10 10 TRUE
360 0 0 TRUE
a11
  • 123
  • 1
    It is the unsigned distance from a nearest multiple of $180$, i.e. the absolute value of the least magnitude remainder mod $180$, i.e. $,\delta' = |\delta \bmod_{\ell}! 180|,,$ where $\bmod_{\ell}!$ uses a balanced residue system (least magnitude remainders). – Bill Dubuque Dec 29 '22 at 09:33

2 Answers2

3

Short answer: $$ \delta' = \bigl\lvert \operatorname{mod}(x - 90, 180) - 90 \bigr\rvert. $$ The graph of $\delta'$ as a function of $\delta$ is a triangle wave. (I'm assuming that this function is periodic every $360$ degrees, but you can restrict the domain to just $[0, 360]$ if you desire.)

Triangle wave.

Sammy Black
  • 25,273
2

It appears that you are looking for a way to specify the reference angle for a given angle $\delta$ expressed in degrees.

Perhaps you should consider$\mod 180$ rather than $\mod 90$.

The reference angle is the positive angle between $\delta$ and the nearest whole multiple of $180$.

There is a unique integer $n$ such that $180n\le\delta<180(n+1)$. That is, such that $n\le\frac{\delta}{180}<n+1$. Using the floor function, we have that $n=\lfloor\frac{\delta}{180}\rfloor$.

So we have $180\lfloor\frac{\delta}{180}\rfloor\le\delta<180\left(\lfloor\frac{\delta}{180}\rfloor+1\right)$

The reference angle $\delta^\prime$ is the smaller of the two positive distances between delta and the two extremes of the inequality.

That is, $\delta^\prime$ is the smaller of $\delta-180\lfloor\frac{\delta}{180}\rfloor$ and $180\left(\lfloor\frac{\delta}{180}\rfloor+1\right)-\delta$.

This gives the definition of the reference angle as follows:

$$ \delta^\prime=\min\left\{\delta-180\left\lfloor\frac{\delta}{180}\right\rfloor,180-\left(\delta-180\left\lfloor\frac{\delta}{180}\right\rfloor\right)\right\} $$

Check and you will find that for angles such as $\delta=90^\circ$ and $\delta=270^\circ$, the value of $\delta^\prime$ will be $90^\circ$.

John Wayland Bales
  • 21,814