$\lim_{n\to \infty }\cos (\pi\sqrt{n^{2}-n})$ - second battle

Question

Followed my question,

I still don't understand why the answers that were given are right.

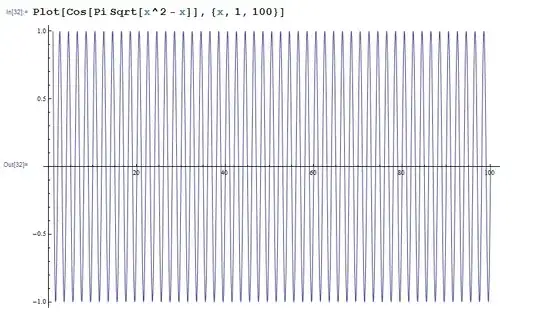
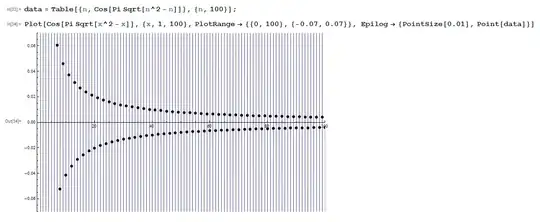
By simply intuition and using the continuity of cosine, we get that we need to compute

$\lim_{n\to \infty}\cos (\pi n\sqrt{1-\frac{1}{n}})$ and because of that, as I see that, there are two clear limits: 1 and -1, and therefore the limit does not exist

Can someone please explain me why am I wrong? two answers that claimed that the limit is 0 got 25 votes together, so I must be mistaken, But still the answers are not satisfying me.

By the way, Wolfarmalpha claims it does not have a limit.

Thank you.

Answer 1

I can sort of see where your conflict arises. Using your intuition, $\sqrt{1-\frac{1}{n}}$ tends to $1$ and so $\cos\big(\pi n\sqrt{1-\frac{1}{n}}\big)$ should hit both $1$ and $-1$ infinitely often. However what you are not taking into account is that as $\sqrt{1-\frac{1}{n}}$ goes $1$, the $n$ term goes to infinity, so this makes no sense as an argument. If we use the Taylor expansion, we find $$ \bigg(1-\frac{1}{n}\bigg)^{1/2} = 1-\frac{1}{2n} -\frac{1}{8n^2} + \dots $$ which gives that $\pi n \sqrt{1-\frac{1}{n}} = \pi n \big(1-\frac{1}{2n} -\frac{1}{8n^2} + \dots\big) = \pi n - \frac{\pi}{2} + O(\frac{1}{n})$. Taking the cosine of this, we get arbitrarily close to zero as $n$ becomes large.

Answer 2

In the other question, you write of letting $x=2\pi k$, but there isn't any $x$, there's only $n$, and the answers you are complaining about are assuming that $n$ is only permitted to take integer values. If the intention is for $n$ to take only integer values, then you can't have $n=2\pi k$, and the upvoted answers are correct. If you want the limit as $n$ goes through the reals, then your argument is correct, and the limit doesn't exist.

Answer 3

The behavior of the sequence $$ \{\cos(\pi \sqrt{n^2-n})\}_{n=1}^\infty $$ and that of the function $$ \cos(\pi \sqrt{x^2-x}) $$ are very different, which has been pointed out by other answers and comments.

I would like to just add three pictures created with Mathematica to illustrate this point here:

Answer 4

To elaborate on Gerry Myerson's answer:

The crucial step in the answer that was upvoted 20 times needs $n$ to only take integer values. The poster used

$$ \cos(\pi(\sqrt{n^2-n}))=(-1)^n\cos(\pi(\sqrt{n^2-n})-n). $$

This works for $n$ an integer, because adding a multiple of $\pi$ only changes cosine by a power of -1. He then works the rest of the problem with some algebra. If $n$ can be any real number, then you can solve the equation

$$ \pi(\sqrt{n^2-n})=k\pi $$

for infinitely many $k$ where $k$ is an odd integer and infinitely many $k$ where $k$ is an even integer. And therefore you get values of -1 and 1 infinitely often. The point is if $n$ is only an integer you can't solve these equations.

Answer 5

[EDITED] You're right that normally we think of cosine as oscillating over all values over the range $[-1,1]$, across the entire real domain. And in that case, your function does not converge.

However, the answers you don't understand, are taking $n$ as increasing through the integers. And over the integers, $\cos(\pi\sqrt{n^2-n})$ behaves very differently to that over reals: because whereas over the reals, the function continues to oscillate over all values in the real range $[-1,1]$, however large $n$ gets, that's not true over the integers.

So, as long as this assumption about $n$ being an integer holds, one may discard any intuition that derives from the behaviour of cosine over the reals.

And over the integers, $\sqrt{n^2-n}$ modulo $1$ converges to $\frac{1}{2}$ as $n\to\infty$, hence, $\cos(\pi\sqrt{n^2-n})$ converges to $\cos\frac{\pi}{2}=0$.