1

I'm familiar with the proof that if the first derivative is always positive then the function is increasing which uses the Mean Value Theorem. How can it be shown that the function not being differentiable at some point does not affect this property? For example a function may have a jump discontinuity with the derivative not being defined at a point but still be increasing.

PrincessEev
  • 43,815
ephe
  • 346
  • Of course not. According to Wikipedia, increasing means monotonically increasing, which is definitely false if the function jumps down. – mathlander Dec 25 '22 at 01:28
  • 1
    I'm not sure I completely understand. If $x$ is a point in the domain of a function $f$ such that $f'(x)$ is not defined, the increasing property may certainly be affected! If the function jumps down at $x$, then $f$ certainly won't be increasing. – Michael Dec 25 '22 at 01:29
  • The result is true if $f$ absolutely continuous (hence differentiable ae) and $f'\ge 0$ where it exists, but the proof is fairly involved as it boils down to proving that the fundamental theorem of calculus holds with the integral of $f'$ being the Lebesgue one and then it's obvious; the counterexamples below are discontinuous – Conrad Dec 25 '22 at 02:22
  • Actually even for $f$ continuous bounded variation the result holds since then $f'$ exists ae but $f(b)-f(a) \ge \int_a^b f'(x)dx$ so we do not necessarily have equality like in the absolutely continuous case but $f'\ge 0$ still implies $f(b)\ge f(a)$ when $b \ge a$ – Conrad Dec 25 '22 at 02:51
  • The Weierstrass nowhere differentiable function $W(x)$ is a continuous function such that at each point where $W'(x)$ exists we have $W'(x) > 0$ (since there are no such points, this is vacuously true), but $W(x)$ is not increasing (or even nondecreasing) at any point (increasing at some point is a much weaker property than increasing in some interval). Of course, more interesting is to consider these properties when the set of points of differentiability is large in various ways. – Dave L. Renfro Dec 25 '22 at 07:34

2 Answers2

4

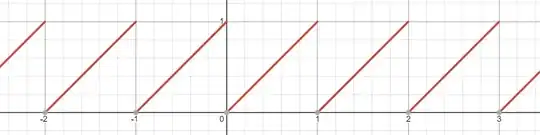
It may not always be the case. Consider the "fractional part" function:

$$f(x) := \{x\} := x - \lfloor x \rfloor$$

This function, in some sense, returns the "decimal part" of $x$. Hence

  • $f(1.5) = 0.5$
  • $f(\pi) = 0.14159...$

...though, for negative numbers, it returns the decimal part in the "other direction":

  • $f(-1.3) = 0.7$
  • $f(-2.1) = 0.9$

...and so on.

The graph itself looks like $y=x$ for $0 \le x < 1$, repeated over and over again:

enter image description here

Where it is differentiable, $f'$ is always positive, but clearly it is not always increasing (because of the times it jumps down).

PrincessEev
  • 43,815
1

Define the function $f$ as $f(x) = x$, if $x<0$ and $f(x)=x-2$ otherwise. Wherever $f$ is differentiable we have $f'(x) = 1 > 0$, but $f$ is not differentiable at $x=0$ (the 'jump discontinuity' you talked about). We have that $f(-1)=-1$ and $f(0)=-2$, so $f(0)<f(-1)$, even though $-1<0$. So this is not true that the function is increasing ---- I suggest you to draw the graph.

Vitor
  • 737