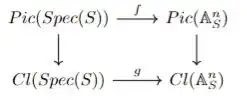Question: Let $S=Spec(\Lambda)$ be a normal affine scheme. Consider the morphism of schemes $\mathbb{A}^{n}_{S}=Spec(\Lambda[x_{1}, \ldots, x_{n}]) \rightarrow S$. Is it true that the induced map $Pic(S) \rightarrow Pic(\mathbb{A}^{n}_{S})$ is an isomorphism?
Some considerations: Since for hypotesis our schemes are normal, I can consider the commutative diagram
($Cl$ is the class group of Weil Divisors) and observe the vertical arrows are injective.
Moreover, the map $g$ is an isomorphism. Actually this follows from the fact there are two types of height one prime ideals in $Spec(\Lambda[x_{1}, \ldots, x_{n}])$: $(x_{i})$ with $1 \le i \le n$ and $\mathfrak{p}$ prime ideal of $Spec(\Lambda)$. But the $(x_{i})$ are principal, so equal to zero in $Cl(\mathbb{A}^{n}_{S})$, and so $g$ is an isomorphism. In particular $f$ is also injective.
I need to prove surjectivity of $f$. Can anybody help me?
Maybe there are also other ways to prove the thesis. Every help is appreciated.