Derivatives cannot have simple discontinuities

Question

A corollary to Theorem 5.12 (Darboux's theorem) in Rudin's PMA is

if $f$ is differentiable on $[a,b]$, then $f'$ cannot have any simple discontinuities on $[a,b]$.

He defines simple discontinuities as follows:

$f$ has a simple discontinuity at $x$ if the right-hand and left-hand limits both exist at $x$.

Rudin does not provide proof. Is this corollary true because any functions with the IVP cannot have simple discontinuities, and not because of other properties of $f'$?

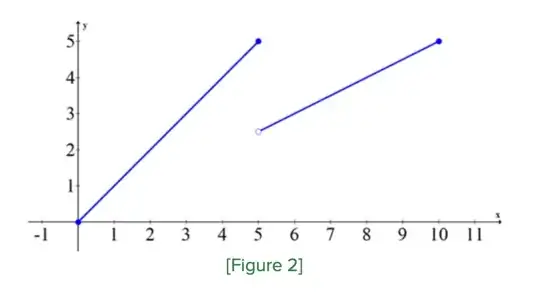
In that case, how about the following function?

If this function is not a counterexample for the converse of the IVT, why is that? Does a function have to have the IVP on every possible open interval in the domain to be considered as a counterexample for the converse of the IVT? That is what I am guessing because I see functions like $f(x)=\sin(1/x)$ for $x\neq 0$ and $f(0)=0$ being used as a counterexample, whose discontinuity at $x=0$ is not a simple discontinuity.

You should define 'simple discontinuity' so that we are all on the same page — FShrike, Dec 20 '22 at 14:04
Is that a graph of $f$, or $f'$? In either case, $f$ is not differentiable at $x=5$. — TonyK, Dec 20 '22 at 14:15
What does derivatives have to do with being a counterexample for the converse of the IVT? — Koda, Dec 20 '22 at 15:09
Your counter-questions don't make sense to me. You know from Darboux's theorem that any derivative satisfies the IVT. That's not a converse, since satisfying the IVT is not the same as being continuous. You want to check that $f'$ has no simple discontinuity, but I still don't know what you mean by that (I know what I mean by that, but conventions vary) — FShrike, Dec 20 '22 at 15:34
Is the reason why the corollary to Darboux's theorem is true because any functions with the IVP cannot have simple discontinuities? In that case, how about the function above? It has the IVP on $[0,10]$ but has a simple discontinuity. — Koda, Dec 20 '22 at 15:47
Does this answer your question? Discontinuities of the derivative of a differentiable function on closed interval — Mittens, Dec 20 '22 at 18:21

score 0 · Accepted Answer · answered Dec 20 '22 at 16:25

A real valued function has the “intermediate value property” if

... for any two values $a$ and $b$ in the domain of $f$, and any $y$ between $f(a)$ and $f(b)$, there is some $c$ between $a$ and $b$ with $f(c) = y$.

With that definition, your function in Figure 2 does not have the intermediate property, it fails e.g. for $(a, b) = (4.5, 5.5)$.

But the following is true:

If $f$ is a real-valued differentiable function on an interval then $f'$ has the intermediate value property. That is Darboux's theorem.
A function with the intermediate value property does not have simple discontinuities.

For the latter, assume that $f$ is discontinuous at $x=a$, and has both a right limit $r$ and a left limit $l$ at $x=a$. Then the three numbers $f(a), l, r$ are not all identical (otherwise $f$ were continuous at that point). In a sufficiently small interval $J = (a-\epsilon, a+\epsilon)$ takes $f$ only values close to $l$, $r$, and $f(a)$, so that $f(J)$ is not an interval. It follows that $f$ does not have the intermediate value property.

I see. So when people look for a counterexample of the IVT, they look for a function $f$ which assumes every value between $f(a)$ and $f(b)$ for ANY $a,b$ in the domain of $f$, not just the endpoints of the domain. It was not clear from Rudin's presentation of the IVT which says that a continuous function $f:[a,b]\to\mathbb{R}$ assumes every value between $f(a)$ and $f(b)$. I thought the function in the figure assumes every value between $f(0)$ and $f(10)$, but has a simple discontinuity, so it is weird. — Koda, Dec 20 '22 at 16:57

Derivatives cannot have simple discontinuities

1 Answers1

Linked