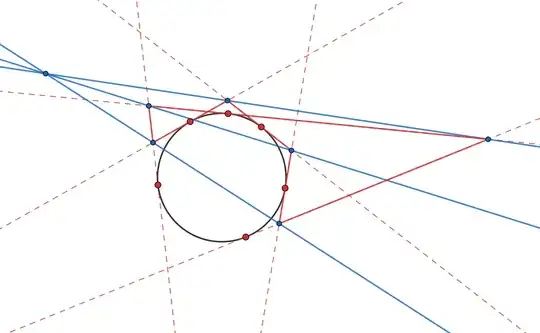
We wish to prove that a $3$-web$^\dagger$ made of tangent lines to a fixed circle $\mathcal{C}$ and the lines through a fixed point $O$ is hexagonal, given the following theorem:
Theorem: A rectilinear $3$-web is hexagonal if it consists of three families of tangent lines to a curve whose dual is cubic.
Let $\mathcal{P}$ and $\mathcal{L}$ denote the sets of points and lines of $\mathbb{P}^2$, respectively. The dual of a conic $$\mathcal{C}=\{p\in\mathcal{P}:p^TAp=0\}$$ is the set of tangent lines $$\mathcal{C}^\triangle=\{l\in\mathcal{L}:l^TA^\triangle l=0\},$$ where $A^\triangle$ denotes the matrix adjugate. By the spectral theorem conics are projectively equivalent up to their signature matrix and since we can pass from nondegenerate to degenerate conics in the limit, all primal (respectively, dual) conics are equivalent in $d$-webs.
Hence we can consider $O$ a real double point of a conic with signature matrix $(+,0,0)$, so that the family of lines through $O$ has multiplicity $2$. Since the dual of $O$ is a real double line the product $O^\triangle\mathcal{C}^\triangle$ is a cubic curve and the result follows from the theorem. This proves Brianchon's theorem:
Theorem (Brianchon): For any six tangent lines $1,2,\cdots , 6$ to a conic, taken as sides of a hexagon, the joins of opposite sides meet in a point.
$\dagger$ Definition: A $d$-web in projective space $\mathbb{P}^n$, or some subset $V\subset\mathbb{P}^n$, consists of $d$ families of smooth level curves, such that no two curves are tangent and exactly one curve from each family passes through every point. Equivalence between $d$-webs is defined up to the differentiable and projective transformations of $\mathbb{P}^n$. A $3$-web is trivial if there exist $f,g,h$ satisfying $f+g+h=0$. A $3$-web is hexagonal if, given any point $p$ and the three curves $f_1,g_1,h_1$ through $p$, when you choose another point $A\in f_1$, then draw $g_2$ through $A$ until you hit $B\in h_1$, then draw $f_2$ though $B$ until you hit $g_1$, etc., you are guaranteed to eventually hit the point $G=A$. A $3$-web of families $F=\{f(x,y)\}$, $G=\{g(x,y)\}$, and $H=\{h(x,y)\}$ is trivial $\iff$ it is hexagonal.