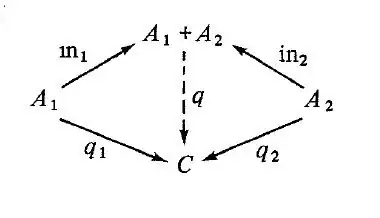
The definition for the disjoint union of two sets are as follow:
Given any pairs $A_1$ and $A_2$ of sets (which may possibly have elements in common) we form the sets $A_1\times \{1\}=\{(a_1,1)|a_1\in A_1\}$ and $A_2\times \{2\}=\{(a_2,2)|a_2\in A_2\}$ which are guaranteed to be disjoint, since whenever $(a,k)=(a',k')$, $k=k'$, so that $A_1\times \{1\}\cap A_2\times \{2\}=\emptyset.$ We then let $A_1 + A_2$ be the union $A_1\times \{1\}\cup A_2\times \{2\}$ - we call it the disjoint union of $A_1$ and $A_2$ because we ensured that the two sets were disjoint before uniting them - and define the maps
$${in}_k :A_k \rightarrow A_1+A_2 :a\mapsto (a,k) \text{ for } k=1,2$$
Along with $q_1:A_1 \rightarrow C$ and $q_2:A_2\rightarrow C$, there exists a unique map $q$ such that $q:A_1+A_2\dashrightarrow C$, defined as $q(a_k, k)=q_k(a_k)$.
If I want to generalize the above definition for a disjoint union of an indexed family of sets.
Does it go as follow:
Suppose we have an indexed family of sets $(A_i|i\in I)$, we form the family of sets $A_i \times \{i\}=\{(a_i,i)|a_i\in A_i, \wedge i\in I\}$. For any pair of sets and each of their respective elements, $(a_i,i)=(a_j,j)$, $i=j,$ so that $A_i\times \{i\}\cap A_j\times \{j\}=\emptyset.$
We let $A_1 + A_2 + \cdots + A_i$ to denote the disjoint union of $A_1 \times \{1\} \cup A_2 \times \{2\} \cup \cdots \cup A_i \times \{i\}.$
We define the family of maps:
${in}_i :A_i \rightarrow A_1 + A_2+ \cdots + A_k :a_i\mapsto (a_i,i) \text{ for } i=1,2,\ldots k$, along with another family of maps: $q_i:A_i\rightarrow C$, $i=1,2,\ldots k.$ There exists a unique map $q$ such that $q:A_1 + A_2+ \cdots + A_k\dashrightarrow C,$ with $q_k=q\circ {in}_k$ and the relation between the maps $q$ and $q_k$ is given by the following identity relation $q(a_k, k)=q_k(a_k)$.
Thank you in advance.