In an 'Estimation Theory' course that I'm taking, I notice over and over that the equations we work with are littered with what I think are called 'Quadratic Forms'. In case that terminology is incorrect, I'm talking about objects of the form: $$ \mathbf{x}^T\mathbf{Qx}$$ or, more broadly: some object, $\mathbf{Q}$, nested between another object $\mathbf{P}$, and its transpose $\mathbf{P}^T$, as $$ \mathbf{P}^T\mathbf{QP} \quad \text{or} \quad \mathbf{P}\mathbf{QP}^T$$
I wonder if there is any notable significance, or some geometrical, visual, or otherwise illuminating interpretation of terms with this structure. In the first example above, of course we classify the matrix $\mathbf{Q}$ as PD, PSD, NSD, ND, or indeterminate, depending on the sign of the form. On an intuitive level, what does this really tell us about how we can conceptualize the matrix $\mathbf{Q}$? Or, the action of the matrix $\mathbf{Q}$?
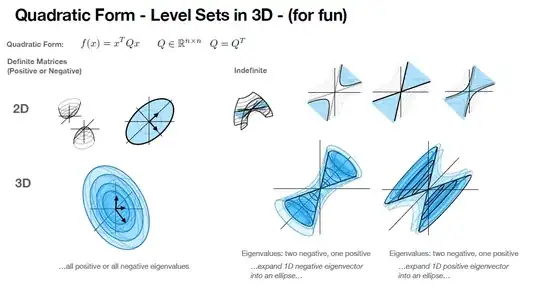
The image below is from a department faculty's publicly published notes on the subject. It makes me wonder more about the connections between these Quadratic Forms, the eigenvalues of $\mathbf{Q}$ and the action of the matrix $\mathbf{Q}$ itself. And, more generally, how we can think about these quadratic forms when the nesting objects are themselves matrices, rather than simple vectors.