Usage of implication arrow in proof steps vs. in logical statements

Question

The implication sign $\implies$ is right associative as I read in multiple sources. (e.g. this answer)

Here $A \implies B \implies C$ means: $$A \implies (B \implies C)$$

But I also see common practices in proof where we chain each step via $\implies$. (e.g. an excerpt here) 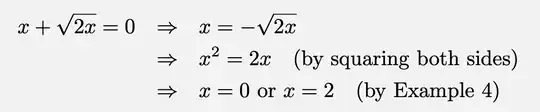Here $A \implies B \implies C$ means: $$(A \implies B) \wedge (B \implies C)$$

Questions

How do we distinguish between these two cases?
What's the alternative to $\implies$ (if it's ambiguous to use)? E.g. thus, ∴, are they interchangeable?

In informal context it denotes a chain of related sequential steps. No real issue... — Mauro ALLEGRANZA, Nov 15 '22 at 08:30
"Thus", "Therefore", "Hence", "which implies", and some others are all standard alternatives to $\implies$. It is common, and often overlooked, that each $\implies$ might be assumed to mean that everything before it implies what follows it. E.g. it may be that $A\implies (A\land B)\implies C$ but that $B$ by itself does not imply $C,$ but someone might write $A\implies B\implies C$ and get away with it. — DanielWainfleet, Nov 15 '22 at 09:17
My reply to #1 is Associativity of logical connectives. My reply to #2 is Implies doesn't mean Therefore. — ryang, Feb 16 '23 at 17:03

Inaccessible Cardinal · Answer 1 · 2022-11-16T19:27:03.227

My logics teachers always told me to differentiate them by using $\rightarrow$ for logical statements and $\Rightarrow$ for proof steps

Also, $A\rightarrow B\rightarrow C$ doesn't exist as a logical statement, it's either $(A\rightarrow B)\rightarrow C$ or $A\rightarrow (B\rightarrow C)$

For example, a theorem would use $\Rightarrow$ (like '$\forall n (n\in\mathbb{N}\rightarrow n≥0)$' ) and a proof of a theorem would use $\Rightarrow$ to guide the reader through its steps

Usage of implication arrow in proof steps vs. in logical statements

1 Answers1