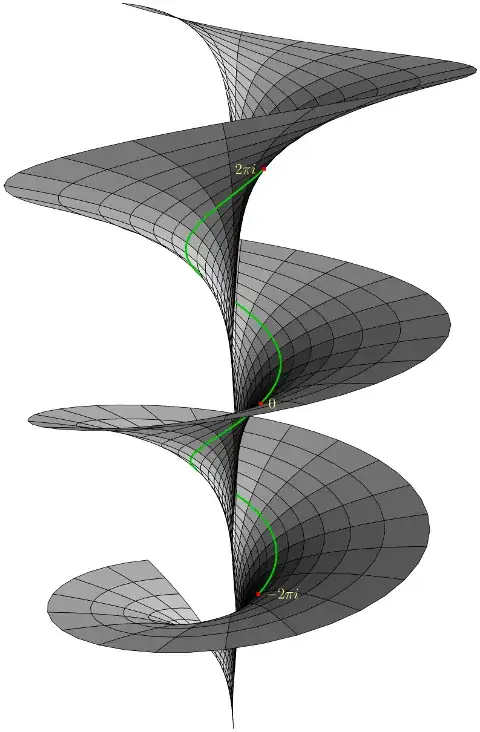
There is not one thing called "the" Riemann surface. Riemann surfaces are a whole class of mathematical objects, just like sets, functions, groups, and manifolds generally.
A Riemann surface most generally is a one-dimensional complex manifold, where the "one-dimensional" means a single complex dimension, so equivalent to two topological dimensions, i.e. the usual way you think of "dimensions" when you say the surface of a sheet of paper or a globe is two-dimensional. That is, it is a two-dimensional surface which, in some sense, can be considered as a "deformed" complex plane while without compromising its essential geometric features. One of these is orientability: a sphere or plane can be a Riemann surface, but a Moebius band cannot, because it in effect would confuse complex numbers with their complex conjugates.
The absence of origin is actually crucial to the "manifold" part in this case. What you are missing in the definition of the manifold is not that "every point in $\mathbb{C}$ has a suitably equivalent neighborhood" but that "every point on the manifold has a suitably equivalent neighborhood" to a plane. The origin is not on the manifold, so whatever happens there doesn't contradict the definition, and in fact it cannot be put on there, because that would indeed break the equivalence: you'd have all the "corkscrew" fanning out from there with a single point floating somewhere along the shaft - it'd not be plane-like at all in any set including that point.
Now as I pointed out, the Riemann surfaces are a whole class of objects. This is not necessarily relevant to your immediate example, but it is very important when it comes to "all complex multi-valued functions". In general, there is no one Riemann surface that can be used to convert a "multi-valued function" (which I prefer to call a one-to-many relation) into a proper function. A good example of a function whose Riemann surface is different from the one you cite is the humble square root $\sqrt{\cdot}$. To understand this, consider the following example. Think of starting at $z = 1$ and $\sqrt{z} = 1$, then rotate counterclockwise to $z = i$, taking care you follow a continuous path in $\sqrt{z}$ as well as $z$. Then $\sqrt{z}$ should go to $\frac{1}{\sqrt{2}} (1 + i)$. Now rotate to $z = -1$. You should expect $\sqrt{z}$ to go to $i$. Rotate again, to $z = -i$, and $\sqrt{z}$ goes to $\frac{1}{\sqrt{2}} (1 - i)$. One more rotation and you're at $z = 1$ again but now $\sqrt{z} = -1$. Now do another full 360-degree rotation. You will be at $z = 1$, but also $\sqrt{z}$ has gone back to $1$.
That is, you have arrived, after wrapping twice around the origin, back to where you started, whereas on the "parking deck" stack of the surface you give, two rotations just takes you to the third "level", which is separate from the first.
In fact, the Riemann surface of the square root doesn't lend itself to so nice a picture - to embed it into a Euclidean space requires a four-dimensional space, $\mathbb{R}^4$ (or if you like, $\mathbb{C}^2$), and that cannot be visualized in a simple and entirely convincing way because our brains don't work well in that. If you take a projection from $\mathbb{R}^4$ to $\mathbb{R}^3$, it will have a self-intersection, and where that is will depend on the viewing angle of the "camera" or "eye" in $\mathbb{R}^4$. You can think of it as somewhat analogous to a trefoil knot. If you forget about the 3D nature of the object and just pay attention to its 2D projection, you will find the 2D projection intersects itself no matter which way the 3D viewer is oriented, but your brain can make sense out of it instinctively as a coherent, non-self-intersecting object. Since our brains are not set up to visualize 4D naturally, you kind of just have to "take it on faith" the intersection is an illusion.
Riemann surfaces can get even more complicated when we consider that some multi-functions have multiple branch points. A good example is $z \mapsto \sqrt{1 - z^2}$. It has two branch points at $\pm 1$, for which a small area around each one looks like the square-root Riemann surface I just described.