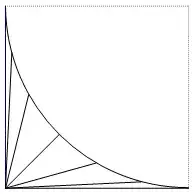
The diagram shows a square of area $An$ and an enclosed quarter-circle.
Line segments are drawn from the bottom-left vertex to points that are equally spaced along the quarter-circle.
The regions enclosed by the line segments and the quarter-circle have areas $a_1, a_2, a_3, ..., a_n$.
Find the value of $A$ such that $\lim\limits_{n\to\infty}\prod\limits_{k=1}^n a_k = 2$.
I have parced the problem to this:
$$\lim\limits_{n\to\infty}\prod\limits_{k=1}^n Anf(k)(g(k)-g(k-1))=2$$
where
$f(k)=\frac{3}{2}-\sin{\frac{k\pi}{2n}-\cos{\frac{k\pi}{2n}}}$
$g(k)=\arcsin{\left(\dfrac{\sin{\frac{k\pi}{2n}}-\cos{\frac{k\pi}{2n}}}{2\sqrt{f(k)}}\right)}$
Desmos suggests $A\approx 5.77987$. I am looking for a closed form for $A$.
I have tried to take the log of the product and relate the resulting sum to an integral, but I do not know how to deal with the $g(k-1)$.
(This question was inspired by a related question, where the product of the lengths of the line segments approaches $2$.)
EDIT
After some more exploration, it seems that $A$ also makes $\frac{1}{n}\prod\limits_{k=1}^{n}A\frac{\pi}{4}\left(\cos{\frac{k\pi}{2(n+1)}}+\sin{\frac{k\pi}{2(n+1)}}-1\right)$ converge to a positive number (approximately $0.8817$).
EDIT2
Based on this question, it seems that $A=\frac{4}{\pi}e^{4G/\pi}\sqrt2$ where $G$ is Catalan's constant.