I couldn't solve this problem, can you help me please?
The Burgers' equation
$$ u_y + uu_x = 0 $$ $ - \infty < x < \infty $ , $ y > 0 $ , $ u(x,0)=f(x) $
My question;
is there any solution $ f(x)= -x $ for all $ y>0 $ , if not, why?
Thank you for your help.
I rewrite equation to common view
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=0$$
There is a solution with each initial value, but this solution exists only for $t\le t_{r}$, where $t_{r}$ is a point where the phenomenon of "rollover" occurs. This phenomenon occurs if some characteristics of this equations intersect. Here is a picture of characteristics:
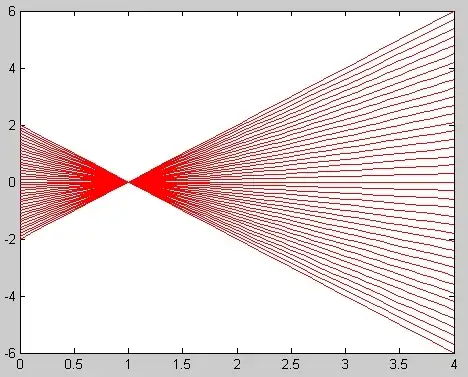
It shows that characteristics of this equations intersect on the moment $t=1$
Before the moment $t=1$ the solution is:
$$u(x,t)=f(x-ut),$$ where $$f(x)=-x $$
After the point $t=1$ the solution does not exist. There you should change your equation to conservation law:
$$\frac{\partial u}{\partial t}+\frac{\partial}{\partial x}\left(\frac{u^2}{2}\right)=0$$
and define the order of this law.
As discussed in the other answers and this post, the method of characteristics yields the classical solution $u = -(x-uy)$, i.e. $$ u(x,y) = \frac{-x}{1-y} \, . $$ Obviously, the denominator vanishes when $y$ reaches unity: the classical solution breaks down as $y\to 1$. This is reflected by the computation of the breaking time $$ y_b = \inf \frac{-1}{(-\text{id})'(x)} = 1 \, . $$ There, all the characteristic curves intersect simultaneously (cf. picture in answer by @cool), i.e. the solution $u$ takes simultaneously all the values from $−∞$ to $+∞$. It literally blows up! There is no weak solution (e.g. of shock-wave type) to start after this blow-up happened.
Follow the method in http://en.wikipedia.org/wiki/Method_of_characteristics#Example:
$\dfrac{dy}{dt}=1$ , letting $y(0)=0$ , we have $y=t$
$\dfrac{du}{dt}=0$ , letting $u(0)=u_0$ , we have $u=u_0$
$\dfrac{dx}{dt}=u=u_0$ , letting $x(0)=f(u_0)$ , we have $x=u_0t+f(u_0)=uy+f(u)$ , i.e. $u=F(x-uy)$
$u(x,0)=-x$ :
$F(x)=-x$
$\therefore u=-(x-uy)=-x+uy$
Since $u(x,y)$ has perfect explicit form $u(x,y)=\dfrac{x}{y-1}$ , of course it has solution for all $y>0$ .
