Meaning of ℝ (\$\Bbb{R}\$)

Question

What is the meaning of "blackboard bold" letters, such as $\Bbb{R}$ (written in MathJax as $\Bbb{R}$ )?

I saw this letter here: MathJax basic tutorial and quick reference

...and in a machine learning text like this:

Any other insight beyond my answer is more-than-welcome. I'm new on this site, and this is my first attempt in life to truly begin to understand the meaning of mathematical symbols.

In college, I was "downvoted" and made fun of too, and my 25k experience on Stack Overflow tells me to expect the same thing here, but keep in mind I'm doing my best here to learn. I'm watching 12 hours of machine learning videos, for heaven's sakes!

I expected the downvote. I was downvoted in college for my questions in-person too. I don't know how else to learn this stuff though. Please provide help and resources to help me figure this stuff out. — Gabriel Staples, Sep 24 '22 at 18:32
I guess the issue is this site expects some certain pre-requisite knowledge — tryst with freedom, Sep 24 '22 at 18:33
The history was that printed books could include bold letters, while professors would be teaching on the blackboard (not sure when that started) and found drawing a single extra stroke was less messy than shading in a whole letter. Common for $Z, Q, R, C$ Eventually it caught on. — Will Jagy, Sep 24 '22 at 18:34
@TrystwithFreedom Hmm. We accept some very basic questions here. It’s more that a willingness to explain the problem is needed. The OP says they know it means the set of reals: so what is the problem? — FShrike, Sep 24 '22 at 18:34
@WillJagy or even a short chalk stick held flat and a single stroke. In typography though, there is a needs to disambiguate fonts. — Weather Vane, Sep 24 '22 at 18:36
@WeatherVane, this is not a puzzling question. I'm asking a straight-forward question looking for a straight-forward, normal math, answer, without pedantic debate. It would be like me asking, "What is zero", and you say, "that's a puzzling question", when all I really need to know is "zero means you have nothing of something"--regardless of the pedantry involved by pedagocic pedantics who would nitpick that to death. — Gabriel Staples, Sep 24 '22 at 18:56
In the context of machine learning, $\Bbb R$ may simply be a stylized way to write R, the computer language. See Introduction to Machine Learning with R. — Weather Vane, Sep 24 '22 at 19:02
Aside: I haven't nit-picked or been pedantic. "Going off on one" or having no SOH will get you ribbed like you were in college. — Weather Vane, Sep 24 '22 at 19:19

score 4 · Answer 1 · answered Sep 24 '22 at 18:34

4

Conventionally $\Bbb R$ is the set of all real numbers. Similarly $\Bbb Z$ is the set of all integers, $\Bbb C$ is the set of all complex numbers, and $\Bbb N$ is the set of all natural numbers. Other number systems use similar notation.

answered Sep 24 '22 at 18:34

Jamie Radcliffe

2,035
1
13
8

This is helpful. Upvoted. Can you be more specific and help me understand concretely what is "the set of all real numbers?" I can tell someone that * in C is a "dereference to a pointer", but that is all meaningless without further explanation. I'd appreciate a longer explanation for each of the things you mentioned. – Gabriel Staples Sep 24 '22 at 18:42
@GabrielStaples Have you read this Wikipedia article? – Xiobiq Sep 24 '22 at 19:02
4

@GabrielStaples: I don't know why you were downvoted; I don't think that was right. That being said, I think that the question you're asking in your comment is distinct enough from your original question to warrant searching this site separately. Your original post is asking about the meaning of the notation $\mathbb{R}$; this comment question is asking about what real numbers are, which is another thing entirely (and much deeper). I'm sure it has been addressed previously, but if you can't find an answer, ask a separate question, thanks! – Brian Tung Sep 24 '22 at 19:02
@BrianTung, sounds good. – Gabriel Staples Sep 24 '22 at 19:05
@GabrielStaples: Note that I have changed my advice to first checking if that question has been asked on this site. I rather suspect it has. But if you don't find a satisfactory answer, ask a new question, but clarify why the existing answers don't help you. – Brian Tung Sep 24 '22 at 19:05
@BrianTung, https://math.stackexchange.com/q/4538280/454133 – Gabriel Staples Sep 24 '22 at 19:19
@GabrielStaples people have gotten very good with this search thing called approach0. You can read about it in the results of https://math.meta.stackexchange.com/search?tab=newest&q=approach0 I seem to remember some examples with precise syntax given among Meta posts. – Will Jagy Sep 24 '22 at 19:54
Let's start with something easier. Do you know what I mean when I say ${\Bbb N} = {1,2,3,4,\dots}$? – Jamie Radcliffe Sep 24 '22 at 21:24
@JamieRadcliffe, no I don't know what you mean by that, unfortunately. I need to learn: A) How do I read that out-loud--meaning: what to say vocally or in my head when I see that, and B) what does it mean. – Gabriel Staples Sep 24 '22 at 21:28

score 1 · Answer 2 · answered Sep 24 '22 at 19:56

In view of your programming background, you can think of the usual number sets as types.

Real numbers are all the numbers we can write with an infinitely long decimal expansion. This is approximated in actual computers with the type "float". Of course this is an approximation because the set of real numbers is infinite but our RAM is finite.

Saying that the distance function maps a pair of images to a real number is akin to a function declaration saying that the distance function takes two arguments of the type "image" and return one element of the type "real".

Gabriel Staples · Answer 3 · 2022-09-24T19:21:18.370

-1

This answer modified for correctness since all 4 downvotes. If still wrong, please explain why. I'd like to fix it.

The best I could find was that $\Bbb{R}$ means "the set of real numbers" (https://en.wikipedia.org/wiki/Blackboard_bold#Usage).

And a "set" is just a collection of "things": https://en.wikipedia.org/wiki/Set_(mathematics).

So, even though "a set of real numbers" could be a list or std::vector<> (in C++) of real numbers, such as this:

$some\_set = \{1, 2, 3, 4, ...\}$

...the set of real numbers is an infinitely-long list of ALL real numbers, including all fractions and fractional numbers, and all numbers with an infinite number of decimal places.

From @Xiobiq's comment with this link: https://en.wikipedia.org/wiki/Real_number:

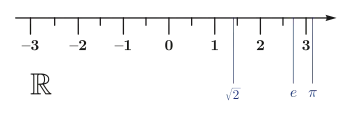
Here are some quotes from the link above (emphasis added):

Real numbers can be thought of as points on an infinitely long number line.

In mathematics, a real number is a value of a continuous quantity that can represent a distance along a line (or alternatively, a quantity that can be represented as an infinite decimal expansion).

The real numbers include all the rational numbers, such as the integer −5 and the fraction 4/3, and all the irrational numbers, such as ${\sqrt {2}}$ (1.41421356..., the square root of 2, an irrational algebraic number). Included within the irrationals are the real transcendental numbers, such as π (3.14159265...).[2] Real numbers can be used to measure (approximately) physical observables such as time, mass, energy; and in one dimension, distance, velocity, acceleration, force, momentum, etc. The set of real numbers is denoted using the symbol R or {\displaystyle \mathbb {R} }\mathbb {R} [3] and is sometimes called "the reals".[4]

edited Sep 24 '22 at 19:21

answered Sep 24 '22 at 18:29

Gabriel Staples

125

No. No computer can handle even the integers, never mind the reals. The reals include $\pi$, for instance, all irrational numbers, etc – FShrike Sep 24 '22 at 18:33
1

It's not "a" set of real numbers, it's "the" set of real numbers. It's all of them, not just some of them. – Amaan M Sep 24 '22 at 18:36
@FShrike, can you explain? I don't know what you mean when you say a computer can't store a set of real numbers. – Gabriel Staples Sep 24 '22 at 18:36
@Filippo, can you please explain? Consider adding an answer. What's a set? What's a field? – Gabriel Staples Sep 24 '22 at 18:37
@AmaanM, ok, now we are getting somewhere. This is useful. I didn't understand that nuance. So, if it is all real numbers, then it is an infinitely long list, and contains numbers with an infinite number of decimal places, right? – Gabriel Staples Sep 24 '22 at 18:37
It's the set of real numbers, not some set. Nothing to do with decimal notation. – Weather Vane Sep 24 '22 at 18:38
@Filippo $\mathbb{R}$ is a set. It is also a group, a ring and a field. Every field is also a set (looking at its elements). – Xiobiq Sep 24 '22 at 18:39
@WeatherVane, I don't understand what you're talking about. I'm going to need a more-thorough answer please. Consider adding an answer. You're talking at a PhD math professor level to a student with only the normal MS in ME level of math background. – Gabriel Staples Sep 24 '22 at 18:41
@Xiobiq "Every field is also a set (looking at its elements)" - Yes, each field has a set associated to it, but this doesn't mean that a field is equal to a set. A field consists of a set and some operations. – Filippo Sep 24 '22 at 18:41
2

@GabrielStaples I mean that you cannot store the (infinite) set of real numbers on a computer, irrespective of their representation. – Weather Vane Sep 24 '22 at 18:43
1

@Filippo Well, this is just being over pedantic for no good reason. To be accurate, actually $\mathbb{R}$ is the set of the real numbers, and not the field. – Xiobiq Sep 24 '22 at 18:50
@Xiobiq I disagree. – Filippo Sep 24 '22 at 18:54
@GabrielStaples To be precise, $\mathbb R$ is actually an ordered field, i.e. a field together with an ordering. And not some arbitrary ordered field, but a complete ordered field. This defines $\mathbb R$ up to a natural isomorphism. Read all about it here. – Filippo Sep 24 '22 at 18:56
As it’s currently written, your answer is unclear. Please [edit] to add additional details that will help others understand how this addresses the question asked. You can find more information on how to write good answers in the help center. – Community Sep 24 '22 at 19:14
@Filippo Well, Wikipedia agrees: "The set of real numbers is denoted using the symbol R or $\mathbb{R}$". Also the general notation (which is also present in this question) is $f:\mathbb{R}\to\mathbb{R}$ which means a function from the set of the real numbers to the set of the real numbers. So, yeah. – Xiobiq Sep 24 '22 at 19:14
@Xiobiq Well, it isn't a surprise that we use the same symbol for the ordered field and the set associated to it, is it? We do this all the time...If I say "Let $V$ be a vector field", then I certainly won't introduce a new symbol for the set associated to $V$ later on... Again, the structure of an ordered field is important because it defines $\mathbb R$ (up to a natural isomorphism...what more can you expect?). – Filippo Sep 24 '22 at 21:36
We can essentially say that $\mathbb R$ is the complete ordered field... – Filippo Sep 24 '22 at 22:20
1

@GabrielStaples there's a lot going on in these comments that's irrelevant to your needs. It's the set of real numbers. It's an infinitely long list. It includes natural numbers like 1, 2, 3, it includes rational numbers like 1.1, 1.2, 1.3, it includes irrational numbers like $\sqrt{2}$ and $\sqrt[3]{2}$ and $\pi$ and $e$, and it includes all of these numbers' negative counterparts. Every number you can think of that doesn't have an $i$ in it. That's all you need. – Amaan M Sep 25 '22 at 16:38
@AmaanM, thank you. Make that an answer and I'll upvote it. – Gabriel Staples Sep 25 '22 at 17:09

Meaning of ℝ (\$\Bbb{R}\$)

3 Answers3