Generalising $ab=\text{hcf}(a,b)\text{lcm}(a,b)$

Question

We have that the product of two numbers is equal to the product of their lowest common multiple (LCM) and highest common factor (HCF): $ab=\text{hcf}(a,b)\text{lcm}(a,b)$. The HCF is alternatively called the greatest common divisor (GCD).

---

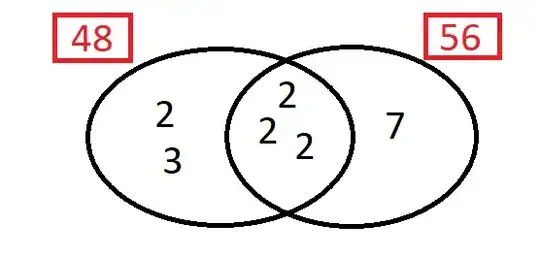
My favourite explanation of this involves Venn diagrams. Make a two-ellipse Venn diagram where ellipse $a$ contains the multiset of prime factors of $a$, and similarly for $b$. The Venn diagram intersection must be the multiset intersection. For instance, if $a=48=2^4\times 3$ and $b=56=2^3\times 7$ then their multiset of prime factors are $\{|2,2,2,3|\}$ and $\{|2,2,2,7|\}$ and this intersects at $\{|2,2,2|\}$, producing this Venn diagram:

We can see that the HCF is the product of the intersection ($2^3=8$), and the LCM is the product of each number in the diagram ($2^4\times 3\times 7=336$). If we multiply HCF and LCM then a number outside the intersection occurs once and a number inside the intersection occurs twice. Additionally, the product of the two numbers involves each number outside the intersection occurring once and each number inside the intersection occurring twice. So the two products coincide (here, $48\times 56=8\times 336=2688$).

---

The question is: what similar equalities exist between the product of three numbers, $abc$, and their pairwise or overall HCFs and LCMs? How can the equalities best be visualised?

Do these patterns extend to $n$ numbers, $a_1,a_2,\dots,a_n$?

Answer 1

Consider the multisets of prime factors $A$ for $a$, $B$ for $b$ and $C$ for $c$. A Venn diagram shows the eight regions $ABC^V:=A\cap B\cap C$, $AB^V:=A\cap B\cap C'$, $A^V:=A\cap B'\cap C'$ and so forth. Here $\emptyset^V:=A'\cap B'\cap C'$ is empty.

In the product $abc$, a number in $ABC^V$ should occur three times, a number in $AB^V,AC^V,BC^V$ should occur twice and numbers in $A,B,C$ should occur once. However, unlike with two numbers, multiplying the HCF by LCM will not give us this: a number in $ABC^V$ would be counted twice and a number in $AB^V,AC^V,BC^V$ would occur once.

However, consider $\text{lcm}(abc)\text{hcf}(ab)\text{hcf}(ac)\text{hcf}(bc)$. This product now includes each number in $ABC^V$ four times (in each term), each number in $AB^V,AC^V,BC^V$ twice (in the LCM and one of the HCFs) and each number in $A,B,C$ once (in the LCM). Now, we need only divide by $\text{hcf}(abc)$ and we have the desired product $abc$.

For example, with $a=300=2^2\times 3\times 5^2, b=144=2^4\times 3^2, c=630=2\times 3^2\times 5\times 7$, we have that $300\times 144\times 630=2721600$ and $\frac{(2^4\times 3^2\times 5^2\times 7)(12)(30)(18)}{6}=\frac{25200.12.30.18}{6}=2721600$.

I will conjecture from here that for $n$ numbers, we have a sort of alternating "inclusion-exclusion" pattern where we have the LCM of all numbers, then multiply by pairwise HCFs, then divide by three-way HCFs, then multiply by four-way HCFs and so forth.