If there is a function $f(x)$ such that f'(x) has a jump discontinuity:
$f(x)=\begin{cases} 2x & 0 \leq x \leq 1 \\ 3x-1 & 1 < x \leq 2 \\ \end{cases} $
then what is the derivative at $x=1$?
The graph looks like this: (orange is $f(x)$ and purple is $f'(x)$)
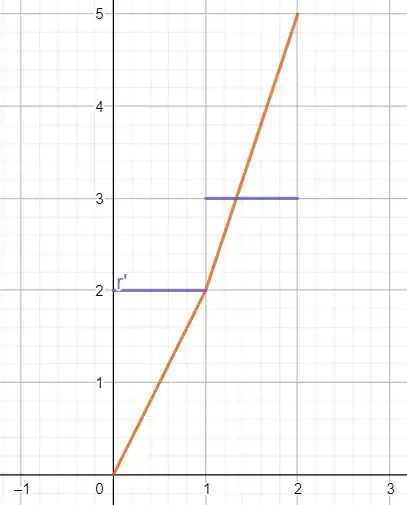
We know that by definition,
$$f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$$
so if the limit fails to exist, the derivative must also fail to exist. (as in, $f$ is not differentiable at $x.$)
Recall also the concept of one-sided limits: $\lim_{x \to a} g(x)$ exists if and only if the one-sided limits $\lim_{x \to a^-} g(x)$ and $\lim_{x \to a^+} g(x)$ exist and agree.
So, let's see what happens when we apply this to our limit definition of $f'(1),$ taking limits from both sides.
Approaching from the left, $h < 0$ implies $1 + h < 1,$ so:
$$\lim_{h \to 0^-} \frac{f(1+h) - f(1)}{h} = \lim_{h \to 0^-} \frac{2(1 + h) - 2}{h} = \lim_{h \to 0^-} \frac{2h}{h} = 2$$
Similarly, approaching from the right, $h > 0$ implies $1 + h > 1,$ so:
$$\lim_{h \to 0^-} \frac{f(1+h) - f(1)}{h} = \lim_{h \to 0^-} \frac{(3(1 + h) - 1)- 2}{h} = \lim_{h \to 0^-} \frac{3h}{h} = 3$$
So, because $2 \neq 3,$ the two one-sided limits don't agree, so the limit fails to exist and $f$ is not differentiable at $1.$
That said, this doesn't mean that all differentiable functions have continuous derivatives: see here for a counterexample.
