Covering unit square with discs; systems of degree-2 polynomials

Question

Given a unit square and $n$ identical circles/discs, what is the smallest radius $r_n$ for which the circles can fully cover the square?

For $n=4$, the proven minimal solution is $r_4 = 1/(2\sqrt2) \approx 0.35355$

For $n=5$, the proven minimal solution is $r_5 \approx 0.32616$

For $n>5$, well, read on.

---

The context behind this is actually pretty thick, and includes:

• Last week's Riddler Classic
• This 2000 paper discussing this covering up to $n=30$, which has been linked in other questions
• My solution in Geogebra to the $5$-circle case

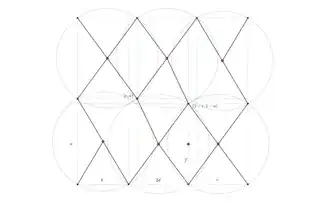Fig 1: $5$-Circle solution with analytic solution (OC)	Fig 2: $6$-Circle solution from Nurmelas & Ostergard, with labels

The $5$-circle result has an analytical solution--though not one that yields a value except via numerical methods--via the following system of polynomials:

$$\begin{cases} a^2 + \frac14 = 4r_5^2 \\ (1-a)^2 + b^2 = 4r_5^2 \\ (2a+2r-1)^2 + (2b-1)^2 = 4r_5^2 \end{cases} $$

The solution is that $a$ is the smaller real root of:

$$64a^6 -144a^5 + 209a^4 -196a^3 +154a^2 -92a +21 = 0$$

and the radius is $r_5 = \textstyle \frac12 \sqrt{a^2 + \frac14}$.

---

Edit: the full minimal polynomial for $r_5$ is degree 12, with $r_5$ being the smaller positive real root:

$$4294967296 r^{12} - 33554432 r^{10} + 213975040 r^8 - 37961728 r^6 - 13421056 r^4 - 152384 r^2 + 180625=0$$

---

Now the $6$-circle solution ought to also have an analytical solution, I would think--if nothing else, a high-degree polynomial. Consider Fig 2. Each of the line segments must be the same length as each of the others--those lengths being the radius of the identical circles. The figure has $C_2$ symmetry. Also note that the sets of four segments in the top left and bottom right connect the four points of a rectangle.

I've added labels to the original figure from the paper. Using those distance labels, this system of equations ought to give us a solution:

$$\begin{cases} a^2 + b^2 = 4r_6^2 \\ (1-a)^2 + c^2 = 4r_6^2 \\ d^2 + f^2 = r_6^2 \\ (c - b - d)^2 + (a - f)^2 = r_6^2 \\ (1 - c - b - d)^2 + (1 - a - f)^2 = r_6^2 \\ b+c+2d=1 \end{cases} $$

The first two equations describe the circles on the corners; the next three describe the segments pointing southeast, northwest, and northeast from the center of the bottom-middle circle, which has its center at $(b+d, f)$.

Nurmelas and Ostergard give the radius as $r_6 \approx 0.29873$. However, both Wolfram Alpha and SageMath return little other than not-smallest solution where we cut the square into six rectangles and circle each of those. Everything else they return either has complex numbers or negative distances.

I'd appreciate any help toward (A) dude, you made a tiny error right here, fix that, or (B) the better way to do it is this, or (C) this won't give you anything solvable, sorry.

I'm actually rather surprised there seem to have been no further papers/computations on this since 2000. Unfortunately, the authors don't give their algorithm or the coordinates of the centers, so it's hard to determine just what they have. My math kingdom for a "Supplementary Material" link.

Answer 1

In 2018, after answering a very similar question to yours on six circles covering a circle, I used an approach quite similar to the Nurmela–Östergard paper – simulated annealing with a mechanically inspired refinement procedure – to find good covers of a circle by up to $25$ circles. When I saw your question I was porting those results from my maths dump Dounreay to Shibuya, the latter recently generalised from its original purpose to store exact solutions to various geometric optimisation problems.

Because the answer is always an algebraic number.

---

The six-circles-covering-square problem (or rather the radius of the circles in the Nurmela–Östergard covering) can be solved much the same way as the six-circles-covering-circle problem. Let the square be $[-1,1]^2$ and define variables as follows:

With $q=(2r_6)^2$ where each circle radius in the picture above is $2r_6$ I have these equations: $$(b-1)^2+(1-a)^2=(b+1)^2+(1-c)^2=4q$$ $$(1-d)^2+((a+c)/2)^2=(2d+(b-1)/2)^2+((1+a)/2-c)^2=q$$ Now I eliminate $d,c,a$ using Singular to get a polynomial $p(b,q)$. I want to minimise $q$, so akin to my six-circles-covering-circle answer I eliminate $b$ in $\{p,p_b\}$ to get $q$'s minimal polynomial:

option(prot); LIB "elim.lib";
ring r=0,(d,c,b,a,q),dp;
ideal I=(b-1)^2+(1-a)^2-4q, (b+1)^2+(1-c)^2-4q,
        (1-d)^2+((a+c)/2)^2-q, (2d+(b-1)/2)^2+((1+a)/2-c)^2-q;
poly p=elim(I,dca)[1];
ideal J=p,diff(p,b);
factorize(elim(J,b)[1]);

Finally the minimal polynomial of $r=r_6$ follows from a simple transformation.

$$513567385819545600000000r^{52}-7761789272975128657920000r^{50}+32231376434429910828711936r^{48}-26408604639265908464812032r^{46}+54549319267072232036499456r^{44}-267434704167110196796588032r^{42}-14725636311941780880162816r^{40}-196340976449037000738865152r^{38}+276544278018037916049178624r^{36}-173942988925278900292550656r^{34}+86285126265400164157120512r^{32}-35908174308785801878306816r^{30}+12801795791889424996180992r^{28}-4090950677420073517967360r^{26}+1145212270252728961751296r^{24}-275128954117684985719808r^{22}+56290606661884343957504r^{20}-9762361232574570924800r^{18}+1430038778302088491648r^{16}-176249085639503139840r^{14}+18147239517089528416r^{12}-1541907874402756800r^{10}+106014873382340000r^{8}-5703051277750000r^{6}+225278951562500r^{4}-5762421875000r^{2}+70556640625=0$$

It is degree $26$ in $q$ and hence degree $52$ in $r$ – monstrously big, but expected since covering problems are very much more algebraically complex than corresponding packing problems, something noted in the Nurmela–Östergard paper. I myself strongly believe the complexity explosion to arise from the system always being underdetermined from static considerations alone, needing differentiated polynomials (a dynamic thing) to fix the optimal solution.

Your assumption that "the sets of four segments in the top left and bottom right connect the four points of a rectangle" is also false; that would correspond to $2a+c=1$ in my variable assignment, while the actual result is $2a+c=0.9785222\dots$

---

The code that produced the exact circle covering picture above is available in Shibuya here.