(This question: Limits of functions at end points of its domain is same as mine but there is no verified answer and had left me more confused. I'll be very thankful if complete answer is provided)
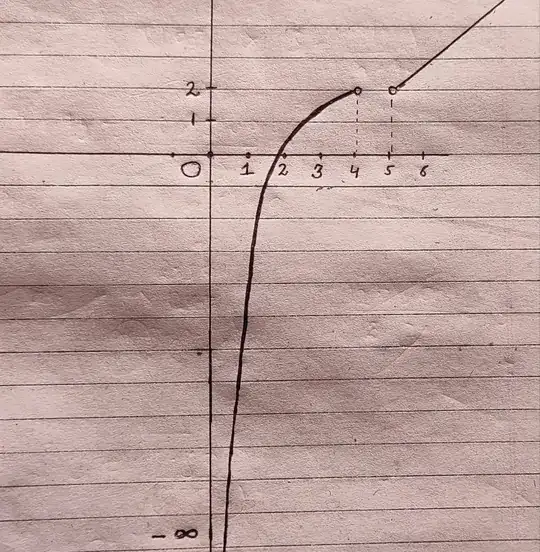 Consider this graph of a function $y=f(x)$ $x ∈ (0,4)∪(5, \infty)$ . I want to know that what is the value of $\lim f(x)$ as :
Consider this graph of a function $y=f(x)$ $x ∈ (0,4)∪(5, \infty)$ . I want to know that what is the value of $\lim f(x)$ as :
$(a)$ $x$ tends to $0$ ( Is it $-\infty$ or limit don't exist ? )
$(b)$ $x$ tends to $5$ ( Is it $2$ or limit don't exist?)
I am having confusion in it from many days. We can't calculate limit from left side in both cases. However, a value approaches if we move from right side only, and in one case it's negative infinity and in one case it's a finite number.
Please clarify it and also tell that how to solve these types of limits if they are provided to us in equations instead of graphical form.