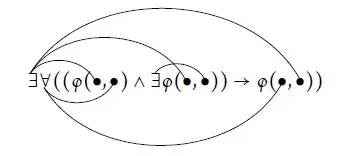
Let $M$ be a model we want to study. The first order language we plan to use is $L$. Now we extend the language $L$ by adding a few constant symbols. Does the supplement of extra constant symbols strengthen our ability to talk about that model $M$?
I'm a newbie to logic, so I'm not sure about it, but I think that depends on the interpretation of the new constant symbols. There are 2 cases:
The interpretation of the new constant symbols are all definable elements of the original language $L$. In this case, even if the new symbols are taken away, we can still make do with the formulas used to define those definable elements, so it makes no difference whether we are supplied these new symbols.
The interpretation of the new constant symbols are not all definable elements of the original language $L$. In this case, we need those new symbols to talk about the undefinable elements, so they strengthens our ability to talk about the model $M$.
Am I correct?
In writing the above question, another problem hit me. What is the model $M$? Where does the model $M$ come from? Must it be something we can get/describe earlier in some language $\Bbb{L}$? Does that have something to do with the above question?