4

While thinking about this question about the Meijer G function, I encountered the following identity listed at https://en.wikipedia.org/wiki/Meijer_G-function#Basic_properties_of_the_G-function (the fifth one in that section) which I have reworked a little bit for clarity:

$$G^{m,n}_{p,q}\left(\begin{matrix}\boldsymbol a \\ (b_1,b_2,\dots,b_{q-1},b_q)\end{matrix}\bigg|~z\right)=(-1)^{b_1-b_q}G^{m,n}_{p,q}\left(\begin{matrix}\boldsymbol a \\ (b_q,b_2,\dots,b_{q-1},b_1)\end{matrix}\bigg|~z\right) \\ \text{when}~m< q~\text{and}~b_1-b_q\in\Bbb Z$$

But this would imply, for example $$G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (0,1,\frac{1}{2},1)\end{matrix}\bigg|~z\right)=-G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (1,1,\frac{1}{2},0)\end{matrix}\bigg|~z\right)$$ Which, due to the permutation symmetry of the Meijer G, means $$G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (0,1,\frac{1}{2},1)\end{matrix}\bigg|~z\right)=-G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (1,1,0,\frac{1}{2})\end{matrix}\bigg|~z\right)$$ And finally, due to the cancellation identity (first identity on the linked Wikipedia page) This would mean $$G^{2,0}_{0,3}\left(\begin{matrix} - \\ (0,1,\frac{1}{2})\end{matrix}\bigg|~z\right)=-G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (1,1,0,\frac{1}{2})\end{matrix}\bigg|~z\right)$$ But this is clearly not the case! In the linked question it is shown, both numerically and analytically, that $$G^{2,0}_{0,3}\left(\begin{matrix} - \\ (0,1,\frac{1}{2})\end{matrix}\bigg|~z\right)+G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (1,1,0,\frac{1}{2})\end{matrix}\bigg|~z\right)=\frac{1}{\sqrt{\pi}}$$

So, I pondered - maybe Wikipedia meant the equality up to a constant difference? That is to say, perhaps the Wikipedia identity should instead read $$\frac{\mathrm d}{\mathrm d z}\left[G^{m,n}_{p,q}\left(\begin{matrix}\boldsymbol a \\ (b_1,b_2,\dots,b_{q-1},b_q)\end{matrix}\bigg|~z\right)-(-1)^{b_1-b_q}G^{m,n}_{p,q}\left(\begin{matrix}\boldsymbol a \\ (b_q,b_2,\dots,b_{q-1},b_1)\end{matrix}\bigg|~z\right)\right]=0 \\ \text{when}~m< q~\text{and}~b_1-b_q\in\Bbb Z\tag{*}$$

To test my hypothesis, I wrote the following little script in Mathematica:

k = 1;
b1 = Round[RandomReal[], 0.01]
b2 = Round[RandomReal[], 0.01]
b3 = Round[RandomReal[], 0.01]
b4 = b1 + k
F[z_] := MeijerG[{{}, {}}, {{b1, b2}, {b3, b4}}, z] - (-1)^
   k MeijerG[{{}, {}}, {{b4, b2}, {b3, b1}}, z]
Plot[Round[F'[z], 10^(-10)], {z, -5, 5}]

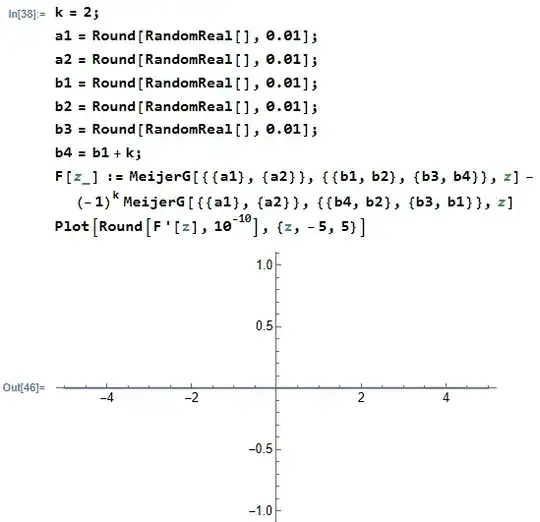
Basically, I generate three random parameters $b_1,b_2,b_3$ that are between $0$ and $1$, and rounded to two decimal places to make the following numerics easier. I then let $k$ be any integer ($1$ in this case) and let $b_4=b_1+k$, so that the difference between $b_1$ and $b_4$ is an integer. (I have set $k=1$ in the above but I find the program produces the expected result for other integer values of $k$ as well.) I then numerically evaluate and plot $$\frac{\mathrm d}{\mathrm dz}\left[G^{2,0}_{0,3}\left(\begin{matrix}- \\ (b_1,b_2,b_3,b_4)\end{matrix}\bigg|~z\right)-(-1)^{b_1-b_4}G^{2,0}_{0,3}\left(\begin{matrix}- \\ (b_4,b_2,b_3,b_1)\end{matrix}\bigg|~z\right)\right]$$

If my proposed formula is right, I would expect the graph to just be a flat line at zero. (I rounded the values to $10^{-10}$ so that it wouldn't output a bunch of machine precision noise.)

And, Lo and Behold, that appears to be the case. I have ran this program several times, for example:

exampleoutput

I even tried putting in some upper parameters, and it still seems to work, for example

example output 2

My questions:

  • Can someone prove that my formula (equation $(*)$) is correct?
  • Is it possible to work out what the constant difference will be in general? Some combination of Gamma functions perhaps?

Thanks in advance.

K.defaoite
  • 12,536

1 Answers1

3

In the definition of the Meijer function, a clear separation of the poles is required: "none of $a_k-b_j$ is a positive integer when $1≤k≤n$ and $1≤j≤m$. This is not the case for the chosen example $$G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (0,1,\frac{1}{2},1)\end{matrix}\bigg|~z\right)$$ When this condition is fulfilled, the given relation seems to hold. For example, one can numerically check that $$G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (2,1,\frac{1}{2},1)\end{matrix}\bigg|~z\right)=-G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (1,1,\frac{1}{2},2)\end{matrix}\bigg|~z\right)$$

Paul Enta
  • 14,113
  • Interesting. Thanks for your input. Again, if we weaken equality to "equality up to a constant difference", can we loosen the requirement for $a_k-b_j\notin \Bbb N$ ? – K.defaoite Sep 13 '22 at 18:08
  • I don't know if we can define the function in this case, there would be an ambiguity for the integration contour. BTW, in the other examples you propose, the relation also holds, for example $$G^{2,0}{0,3}\left(\begin{matrix}- \ (1,2,3,4)\end{matrix}\bigg|~z\right)+G^{2,0}{0,3}\left(\begin{matrix}- \ (4,2,3,1)\end{matrix}\bigg|~z\right)=0$$ the differentiated relation is then true... – Paul Enta Sep 13 '22 at 19:57
  • Well, Mathematica must have a way that it does it - I'd imagine via the representation using hypergeometrics - because it has no issues when I put in Meijer G functions having upper and lower arguments differing by an integer. – K.defaoite Sep 13 '22 at 20:04
  • In this page, the representation through hypergeometric functions is to be taken carefully as there are $\Gamma(1-a_j+b_k)$ terms in the prefactors. I don't know how Mathematica (or Maple too) evaluate the function. – Paul Enta Sep 13 '22 at 20:17
  • 1
    Okay, I will look into it. Thanks for what you've given me so far. Unfortunately I cannot accept your response as it does not completely answer my question, but I have upvoted it. – K.defaoite Sep 13 '22 at 20:22
  • Related. – K.defaoite Sep 14 '22 at 21:40