I need to prove that there exist no solutions apart from $(0,0)$ and $(2,2)$ through infinite descent. I understand the premise of descent, and was even able to solve another similar question. A small hint would be appreciated, as this presently has me stumped and I just can't figure it out. I've tried taking $x = 2x_1, y = 2y_1$, but to no avail as I seemingly can't get back the original equation by doing so. Is there a flaw in this logic?
-
Hint: for larger integers $x+y<2\max(x,y)$. – QC_QAOA Sep 01 '22 at 14:10
-
I understand it's part of the question, but infinite descent is really overkill. If $b$ divides $x$ but not $y$ (or $y$ but not $x$) we immediately find a contradiction, so $x=y$. Then $2x=x^{2}$ which is trivially solved. – Andijvie Sep 01 '22 at 14:15
-
Hint for other cases: Both negative obviously false, one positive one negative, $|x+y|<|x|+|y|\leq 2 \max(|x|,|y|)$ – Alan Sep 01 '22 at 14:16
-
@Andijvie: all we can deduce from your argument by contradiction is that $x=\pm y$. I realise that $x=-y$ is easy to rule out, but you should at least mention it. – TonyK Sep 01 '22 at 16:14
-
@QC_QAOA, could you please elaborate on the hint? I'm unsure as to how to use it – Sep 01 '22 at 22:28
4 Answers
One should always have a feel of the problem. In this case, the finiteness of solutions is not due to number-theoretic properties (e.g. $4m=2n+1$ has no solutions for number-theoretic properties), but because of size. Adding two numbers is generally much smaller than multiplying them. So the solutions will be confined to small numbers.
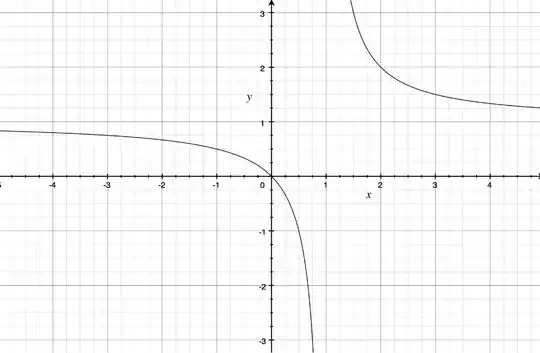
To make this precise, rewrite the equation when both $x$ and $y$ are non-zero: $$\frac1x+\frac1y=1$$ This is much clearer, for if two numbers are to add up to one, at least one is greater than or equal to 1/2. This means at least one of the number is either 1 or 2. This gives all the solutions.
Can you take it from here?
- 4,575
-
-
@asdf256 There is no descent here. By the way in my opinion this answer is more natural than infinite descent. – PNT Nov 12 '22 at 19:54
$\rm\color{#c00}{Descent}$ is via $\rm\color{#0a0}{reflection}$ symmetry on hyperbola $\,\cal C\!: x+y = xy,\,$ i.e. $(x,y)$ on $\cal C\Rightarrow \color{#0a0}{(y,x)}$ on $\cal C$. Thus if $\,(a,b)\in\Bbb N$ and $(a,b)$ on $\,{\cal C}\,\ \color{#90f}{{\rm has}\ a> 2}$ then $\,\color{#c00}{b < a}\,$ so its reflection $\color{#0a0}{(b,a)}$ has $\rm\color{#c00}{smaller}$ $x$ coordinate. We can repeat this descent step again on $(b,a)$ and again $\,\ldots$ (i.e. infinite descent) since $\color{#90f}{{\rm also}\ b > 2}$ (else we get contradictions: $\,b\!=\!2\Rightarrow a\!=\!2;\ $ $b\!=\!1\Rightarrow a\!+\!1 = a;\ $ $b\!=\!0\Rightarrow a\!=\!0)$.
Remark $ $ Generally (reflection) symmetries govern descent on integer points on conics - see the links I give here in the context of less trivial Vieta jumping reflection symmetry.
$$\bbox[5px,border:2px solid #000]{\text{the hyperbola}\,\ x+y = xy}$$
- 272,048
-
There are of course quicker ways to deduce contradictions from the hypothesis that there is an integer point $(a,b)$ with $a > 2$ (e.g. using the stronger $a>2\Rightarrow \color{#c00}{b < 2})$ but the point of the above is to show how it can be viewed as a special case of general descent methods for conics. – Bill Dubuque Sep 02 '22 at 20:11
-
this is really beautiful and eye-opening. thanks a lot for this post. i wish i could verify two solutions. – Sep 03 '22 at 00:01
Write: $y = x(y-1)$. This shows $x \mid y$. Thus let $y = kx, k \in \mathbb{Z}$. Substitute $kx$ back into the equation for $y$: $kx = x(kx-1) = kx^2-x$. Observe that $x = 0$ is a solution and thus $y = 0$ as well in the original equation. So $(0,0)$ is a solution. Besides this, for $x \neq 0$, $k = kx-1\implies 1 = k(x-1)\implies k \mid 1\implies k =\pm 1$. If $k = 1 \implies y = x \implies 2x = x^2\implies x(x-2) = 0 \implies x = 0,2$. Thus another solution is $(2,2)$. If $k = -1 \implies x = -y \implies xy = x+y = 0 \implies x = 0$ or $y=0$. Either one gets back to $(0,0)$ being a solution and this is already accounted for. So there are $2$ solutions: $(0,0), (2,2)$.
- 6,390
-
I'm not quite sure how this particular solution is in the "spirit" of infinite descent, it seems like just algebra to me; I've done something similiar to derive my solution, but I don't get how I would prove it using descent – Sep 01 '22 at 22:24
Here is the Infinite Descent solution: Observe that $x$ must be even. For if $x$ were odd, then if $y$ is odd, then $x+y$ is even while $xy$ is odd. Thus there is no solution. If $y$ is even, then $x+y$ is odd and $xy$ is even. Thus there is no solution either. Now with $x$ being even, then $y = x(y-1)$ is also even. Thus we might let $x = 2x_1, y = 2y_1$ where $x_1,y_1 \in \mathbb{Z}$. Substituting $2x_1,2y_1$ for $x,y$ respectively into the equation, we have: $2x_1+2y_1 = 4x_1y_1\implies x_1+y_1 = 2x_1y_1$. Observe that if $x_1$ or $y_1$ is odd, then both are odd. We have: $2 = \dfrac{x_1+y_1}{x_1y_1}= \dfrac{1}{x_1}+\dfrac{1}{y_1}\le 1+1 = 2$. Thus equality occurs when $x_1 = y_1 = 1$. This gives $x = y = 2$. So if either is even then both are even. Thus again we have: $x_1 = 2x_2, y_1 = 2y_2$, and substituting this into the new equation: $2x_2+2y_2 = 4x_2y_2 \implies x_2+y_2 = 2x_2y_2$. Observe at this point that $x_2,y_2$ must be both even. For if one is odd, then the other is odd too and for this we already processed it and have that $x_2 = y_2 = 1$ if they are both odd, hence $x_1 = 2 = y_1$. But this can't occur since it violates the equation: $x_1+y_1 = 2x_1y_1$ above. Thus we have that $x_2,y_2$ are both even, and we can repeat this process indefinitely which yields a contradiction because it must stop at some point. In brief, we have again $2$ solutions: $(x,y) = (0,0), (2,2)$.
- 6,390