I am trying to understand how the inverse trigonometric identities below work/are derived: $$\tan^{-1}(x)+\tan^{-1}(y)=\tan^{-1}\left(\frac{x+y}{1-xy}\right)\\ xy<1$$ The above identity has a proof that depends on the identity for $\tan(x)+\tan(y)$, which I have seen in my textbook, and I understand.
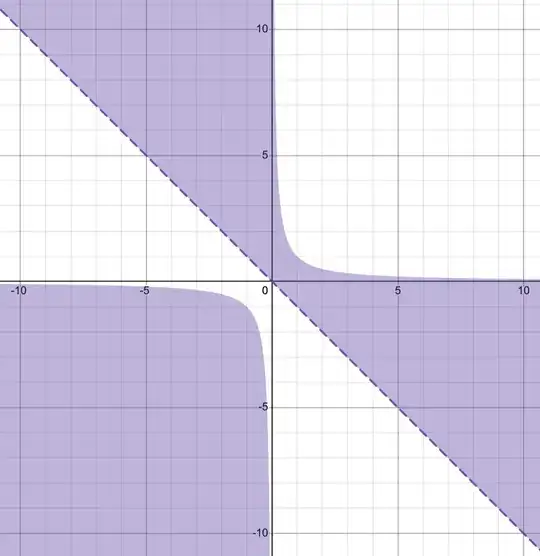
$$\tan^{-1}(x)+\tan^{-1}(y)=\pi + \tan^{-1}\left(\frac{x+y}{1-xy}\right)\\xy>1$$ This one is mentioned in the book, but not proved.
I can understand the logic behind it, since
- if the angles related to $x$ and $y$ are such that the angle related to $x+y$ will be in the second quadrant, then it is not possible for the $\tan^{-1}$ to ever give a correct output
- For $x>0,y>0$ if $xy>1$, then $1-xy<0\Rightarrow\frac{x+y}{1-xy}<0$, and that will give an answer in the fourth quadrant, whereas we likely want one in the second quadrant.
However, this is just intuition. Some questions I have:
- where does the $xy>1$ come in? How is it established/proved?
- where does the $\pi$ factor come in?
- is it possible to see a complete proof for both cases of the property.