The hardest geometry question with "a triangle" and "a circle" - Circle intersecting triangle equally in 5 parts

Question

I received this question long time ago from one of my old friends who is mathematician/physicist. He called it the hardest geometry question with "a triangle" and "a circle". I am not sure if he know the answer or not. Here it is.

Note: These picture are just the example of possible answer. The actual answer might look like one of these or not like any of these.

The circle intersects the triangle and divides the area into 5 parts. Each 5 parts of the red-fill areas have equal area. The radius of circle is 1.

That is all the information the question gives. Then the question asks these two things.

• Find the distance from the center of the circle to the centroid of the triangle. If there are more than 1 possible solutions, find longest and shortest possible the distance from the center of the circle to the centroid of the triangle.
• Find length of outer perimeter of the new intersecting shape. If there are more than 1 possible solutions, find longest and shortest possible length of outer perimeter of new intersecting shape.

Note : If you think that there is only 1 possible solutions that the triangle is isosceles, you also have to proof that there is really only 1 possible solutions.

I have to say that I don't even know how to start to solve this question. The question doesn't even specify the type of the triangle. I think the triangle has to be isosceles triangle, but I remember that the question doesn't specify it.

Edit: I realize where I get this question from. And for now, I doubt if the triangle has to be isosceles or not.

Edit(2) : Due to some technical reason, the account of the real original poster is merged to my account. That is why there is a delay of the update on this question. I do contact and take to the real original poster. Here is why he edit this question.

After sometimes, I decide to change the original question a bit by adding more picture. The original question is actually tricky that give only the first image and trick anyone who try to solve it that that is how the answer look like. R. J. Mathar and John Bentin answer is good but that isn't what the original question ask for.

Edit(3) : The question might not have analytical solution. So, if there is no analytical solution, numerical solution is acceptable.

Answer 1

The ansatz for the left-right symmetric case of the illustration is like this: Circle Radius is $R$ and center of coordinates is at $x=y=0$ at the circle center. Top vertex of the triangle is at $x=0$, $y=y_0$. Right/East vertex of the triangle at $x=x_1$, $y=y_1<y_0$. Left/West vertex of the triangle at $x=-x_1$, $y=y_1$. Full circle area is $A\equiv \pi R^2$.

The line from the $\vec r_0=(0,y_0)$ to $\vec r_1=(x_1,y_1)$ has the parameter representation $\vec r=\vec r_0+t(\vec r_1-\vec r_0)$ where $0\le t\le 1$ is the unitless distance along the line. Cartesian components of points on the line are \begin{equation} r_x= 0+t x_1;\quad r_y = y_0+t(y_1-y_0). \end{equation} This intersects the circle of $x^2+y^2=R^2$ at some specific $t_0$ given by \begin{equation} (t_0x_1)^2 + [y_0+t_0(y_1-y_0)]^2 = R^2 \end{equation} \begin{equation} t_0^2[x_1^2+(y_1-y_0)^2] +2t_0y_0(y_1-y_0)+y_0^2-R^2 =0 \end{equation} which is a quadratic equation for $t_0$ which can be solved if the $x_1, y_0, y_1$ are known. Unitless coordinates are $\hat x_1\equiv x_1/R$, $\hat y_1\equiv y_1/R$, $\hat y_0\equiv y_0/R$, so \begin{equation} t_0^2[\hat x_1^2+(\hat y_1-\hat y_0)^2] +2t_0\hat y_0(\hat y_1-\hat y_0)+\hat y_0^2-1 =0 \end{equation}

The wedge-shaped upper part of the circle (outside the triangle) has the area \begin{equation} A_u = 2\int_0^{t_0x_1} dx \int_{y_0+t(y_1-y_0)}^{\sqrt{R^2-x^2}} dy,\quad x=tx_1 \end{equation} where the factor 2 means we are computing only the eastern part of the left-right symmetric area. We integrate upwards from the edge of the triangle up to the circle's perimeter. \begin{equation} A_u = 2\int_0^{t_0x_1} dx \int_{y_0+x(y_1-y_0)/x_1}^{\sqrt{R^2-x^2}} dy \end{equation} \begin{equation} = 2\int_0^{t_0x_1} dx [\sqrt{R^2-x^2} - y_0-x(y_1-y_0)/x_1] \end{equation} \begin{equation} = 2\int_0^{t_0x_1} dx \sqrt{R^2-x^2} +t_0x_1[t_0(y_0-y_1)-2y_0] \end{equation} \begin{equation} = 2[\frac12 x\sqrt{R^2-x^2}+\frac12 R^2\arctan\frac{x}{\sqrt{R^2-x^2}}]\mid _0^{t_0x_1} +t_0x_1[t_0(y_0-y_1)-2y_0] \end{equation} \begin{equation} = [ x\sqrt{R^2-x^2}+ R^2\arctan\frac{x}{\sqrt{R^2-x^2}}]\mid _0^{t_0x_1} +t_0x_1[t_0(y_0-y_1)-2y_0] \end{equation} \begin{equation} = t_0x_1\sqrt{R^2-(t_0x_1)^2}+ R^2\arctan\frac{t_0x_1}{\sqrt{R^2-(t_0x_1)^2}} +t_0x_1[t_0(y_0-y_1)-2y_0]. \end{equation} One requirement set by the problem is $A_u=A/3$,. \begin{equation} t_0x_1\sqrt{R^2-(t_0x_1)^2}+ R^2\arctan\frac{t_0x_1}{\sqrt{R^2-(t_0x_1)^2}} +t_0x_1[t_0(y_0-y_1)-2y_0] = \frac13 \pi R^2. \end{equation} \begin{equation} t_0 \hat x_1\sqrt{1-(t_0\hat x_1)^2}+ \arctan\frac{t_0\hat x_1}{\sqrt{1-(t_0\hat x_1)^2}} +t_0\hat x_1[t_0(\hat y_0-\hat y_1)-2\hat y_0] = \frac13 \pi \end{equation}

The area in the triangle is half the baseline times the height, \begin{equation} A_t = x_1(y_0-y_1) \end{equation} and the requirement set by the problem is $A_t=A$, \begin{equation} x_1(y_0-y_1) = \pi R^2 \end{equation} \begin{equation} \hat x_1(\hat y_0-\hat y_1) = \pi \end{equation}

The area inside the circle and below the triangle is the usual equation of a circular segment where $y_1$ specifies how much is left. Sagitta $h\equiv R+y_1$, \begin{equation} A_b= R^2\arccos(1-\frac{h}{R})-(R-h)\sqrt{R^2-(R-h)^2}, \end{equation} and the requirement set by the problem is $A_b=A/3$, which yields \begin{equation} R^2\arccos(1-\frac{h}{R})-(R-h)\sqrt{R^2-(R-h)^2}=\pi R^2/3, \end{equation} \begin{equation} \arccos(1-\frac{h}{R})-(1-h/R)\sqrt{1-(1-h/R)^2}=\pi /3,\quad h/R=1+\hat y_1. \end{equation} \begin{equation} \arccos(-\hat y_1)+\hat y_1\sqrt{1-\hat y_1^2}=\pi /3. \end{equation} So this is solved by $\hat y_1\approx -0.26493208460277686243411649$ see for example https://oeis.org/A192408 .

The result is given numerically by searching for the root of equation from the requirement of $A_u$. $\hat y_1$ is already given. For each $y_0$ a $\hat x_1$ is immediately given from the requirement of $A_t$, then $t_0$ is given by solving the aforementioned quadratic equation, and the root for $A_u$ is computed with the Newton-method starting at $y_0\approx 0.3$, the result is \begin{equation} y_0\approx 0.31732443412475189342498268 \end{equation} \begin{equation} x_1\approx 5.395547413458714328330188 \end{equation} \begin{equation} t_0\approx 0.1811308455334911005772355 \end{equation} The height of the triangle is \begin{equation} H=y_0-y_1 \approx 0.582256518727528755859 \end{equation} The two acute angles of the triangle are given by $\arctan(H/x_1)$, \begin{equation} \alpha \approx 0.107498260413536413743 rad \approx 6.159196626693887913^\circ \end{equation} The long side has length \begin{equation} s_l=2x_1\approx 10.79109482691 \end{equation} The 2 short sides have lengths \begin{equation} s_s=\sqrt{H^2+x_1^2}\approx 5.426873367278964196805 \end{equation} Heron's formula gives for the incircle radius \begin{equation} r_i = 0.2902855763270050753515052, \end{equation} which means it is $y_1+r_i\approx 0.0253534917242282129173$ away from the circle center. The diameter of the circumscribed circle (which touches all 3 vertices of the triangle) is given by the ratio $d_u=s_s/\sin \alpha\approx 50.5807210348528797132$. The distance of the centroid to the circle center is $d_u/2-y_0\approx 24.9730308.$ The intersection of the two short sides by the circle have coordinates $r_x=t_0x_1\approx 0.9773000651158178$ and $r_y=y_0+t_0(y_1-y_0)\approx 0.2118598185702$. Measuring angles from the circle center horizontally ccw gives an azimuth $\tan \alpha=r_y/r_x$ with $\alpha_1\approx 12.2313646678072392^\circ$. The intersection of the long side by the circle has coordinates $y_1$ and $\sqrt{1-y_1^2}$. The $\arctan$ of the ratio gives an azimuth of $\alpha_2\approx -15.36291729414711137^\circ$ for that intersection. The perimeter of the circle that is not inside the triangle is $2R(\pi-(\alpha_1-\alpha_2))\approx 5.31996315726001831$ where the two angles are measured in radians and the factor 2 accounts for the east and west sections.

There is some indication that this is the only solution because starting the Newton iteration for any initial value of $y_0$ from 0.01 to 0.99 in steps of 0.01 always converges to that same solution. Of course the other sign (triangle flipped upside down) is also a solution.

Answer 2

There are enough degrees of freedom in this problem to choose the triangle to be isosceles and symmetrically placed with respect to the circle, as you have done, for simplicity. Choose units so that the radius of the circle is $1$. Cut the diagram symmetrically in half with a line through the centre of the circle and the apex of the triangle, which perpendicularly bisects the base of the triangle.

Let us measure angles around the circle anticlockwise from the downward ray of the bisector. Say the base cuts the circle at a point with circular angle $\alpha$, while the right-hand apical side meets the circle where the corresponding angle is $\theta$. From the given equality of areas, we get $$\alpha-\cos\alpha\sin\alpha=\tfrac13\pi.\qquad\qquad(1)$$After some comparison of areas, from the given conditions, we can obtain $$(\tfrac23\pi-\theta+\cos\alpha\sin\theta)^2=\pi(\tfrac23\pi-\theta+\cos\theta\sin\theta).\quad(2)$$ Now, mixed algebraic–trigonometric equations like these cannot be solved by Euclidean geometry. The best we can do is use a numerical approach, such as Newton–Raphson, first by finding $\alpha$ to the required degree of accuracy from eqn 1 and then solving eqn 2 using this value of $\alpha$.

Uniqueness of solution: Equation 1 may be written $$\sin2\alpha=2\alpha-\tfrac23\pi.$$ For $0<\alpha<\frac13\pi$, the LHS is positive while the RHS is negative. In the interval from $\frac13\pi$ to $\frac12\pi$, the LHS continually decreases, with negative gradient, from $\frac12\surd3\approx0.866$ to $0$, while the RHS correspondingly increases, with positive gradient, from $0$ to $\frac13\pi\approx1.047. $ Hence there is a unique solution for $\alpha$ in this interval. Between $\frac12\pi$ and $\pi$, there is again a mismatch of sign between the sides. Therefore the solution for $\alpha$ is unique: Newton–Raphson gives $\alpha\approx1.302663$, with $\cos\alpha\approx0.264932$.

By the orientation of the triangle, $\theta>\alpha$. In the range $\alpha<\theta<\frac12\pi$, the LHS of eqn 2 is no more than $(\frac23\pi-\alpha+\cos\alpha)^2\approx1.12$, while the RHS decreases to a minimum of $\frac16\pi^2\approx1.645$. So the solution lies above $\theta=\frac12\pi$, where the LHS decreases (tangentially) to its minimum value $0$ at $\theta=\beta\approx2.293159$. At that point, the RHS is negative, so the solution is in the range $\frac12\pi$ to $\beta$. In this range, the LHS is increasing while the RHS is decreasing. It follows that the solution for $\theta$ is unique.

The general case: Five parameters need to be fixed to specify a triangle in a plane, given a reference orientation, but only four constraints in the conditions are given for the areas. Hence there is a one-dimensional space of solutions if we drop the requirement that the triangle is isosceles. A manageable case is the one where two sides trisect the circle while the other lies outside the circle. While I don't think that this would be significantly harder to address than the symmetric case, it naturally forms a separate question, which should be posted as such. The asymmetric case where a vertex lies inside the circle looks ugly to me, and not much fun to answer. The borderline case where a vertex lies on the circle is as easy to deal with as the symmetric case, with a specific solution. Again, that should be posted as a separate question.

Answer 3

We prove here the non-unicity of the required triangles. It is clear that if two circular segments on a circle have same area, also have same length of chord. In the unitary circle we are concerned with two disjoint circular segments having area $\dfrac{\pi}{3}$ because the circle has area equal to $\pi$. The involved chord have length, noted $a$, given by the system

$$\dfrac{\theta-\sin(\theta)}{2}=\dfrac{\pi}{3}\\a=2\sin\left(\frac{\theta}{2}\right)$$ from which we have the data for the problem to solve (see at attached figure) $$\begin{cases}\theta\approx 2.60533\\ a\approx 1.92853529\end{cases}$$

To determine the outer region having area equal to $\dfrac{\pi}{3}$ we have five unknowns, , $\alpha,\beta, \gamma,x$ and $y$ for which we have the following system of five equations. $$\begin{cases}2\theta+\beta+\gamma=2\pi\\\\\alpha=\dfrac{\gamma-\beta}{2}\\\\(a+y)y=(a+x)x\\\\\dfrac{xy\sin(\alpha)-(\beta-\sin(\beta))}{2}=\dfrac{\pi}{3}\\\\(2\sin(\beta))^2=x^2+y^2-2xy\cos(\alpha)\end{cases}$$ From which $\gamma=\pi-\theta+\alpha=0.536262653+\alpha$ and $\beta=\pi-\theta-\alpha=0.536262653-\alpha$.

Put for confort $A=0.536262653$ and $B=\dfrac{2\pi}{3}=2.0943951$ so we have the system of three unknowns. $$\begin{cases}(a+y)y=(a+x)x\\\\{xy\sin(\alpha)-A+\alpha+\sin(A-\alpha)}=B\\\\\left(2\sin(A-\alpha)\right)^2=x^2+y^2-2xy\cos(\alpha)\end{cases}$$ Note that $y=x$ because the chords $\overline{AB}=\overline{CD}$ (or because $(a+y)y=(a+x)x\iff(y-x)(y+x-a)=0)$ so we have the resultant in $\alpha$

$$x^2=\dfrac{B+A-\alpha-\sin(A-\alpha)}{\sin(\alpha)}=\dfrac{2\sin^2(A-\alpha)}{1-\cos(\alpha)}$$ i.e. $$\dfrac{2.6306577-\alpha-\sin(0.5362626-\alpha)}{\sin(\alpha)}=\dfrac{2\sin^2(0.5362626-\alpha)}{1-\cos(\alpha)}$$ from where we get $\alpha\approx 0.203$ radiands.

This value of $\alpha$ determines the position of point $P$ in the figure because the chord $\overline{AB}$ should have constant length $a\approx 1.92853529$ (optionnally one can calculate $x$ having $\alpha$). This position of vertex $P$ is unique because if the point $A$ change of position then the outer region $PBD$ becomes larger or smaller than $\dfrac{\pi}{3}$.

Regarding the other outer part of the triangle, that one with two vertices, the mean value theorem ensures the existence of a lot of possible shapes according with the angle we consider between two sides of the triangle. The effective calculation I suppose can be made in analogous way to that for region $BDP$.

Answer 4

Starting from @John Bentin's answer, the zero of function $$f(\alpha)=\sin(2\alpha)-2\alpha+\frac23\pi$$ can be obtained using a series expansion around $\alpha=\frac \pi 2$.

$$f(\alpha)=-\frac{\pi }{3}-4 \left(\alpha -\frac{\pi }{2}\right)+\frac{4}{3} \left(\alpha -\frac{\pi }{2}\right)^3-\frac{4}{15} \left(\alpha -\frac{\pi }{2}\right)^5+O\left(\left(\alpha -\frac{\pi }{2}\right)^7\right)$$ Using series reversion, then

$$\alpha=\frac{\pi }{2}-\frac{1}{4} \left(f(\alpha)+\frac{\pi }{3}\right)-\frac{1}{192} \left(f(\alpha)+\frac{\pi }{3}\right)^3-\frac{1}{3840}\left(f(\alpha)+\frac{\pi }{3}\right)^5+O\left(\left(f(\alpha)+\frac{\pi}{3}\right)^7\right)$$ So, since we need $f(\alpha)=0$, the approximation $$\alpha \sim\frac{5 \pi }{12}-\frac{\pi ^3}{5184}-\frac{\pi ^5}{933120}=1.30269$$ while Newton method gives $\alpha=1.30266$.

Using the first series, it gives $$\cos(\alpha)=\frac{1}{4} \left(f(\alpha)+\frac{\pi }{3}\right)+\frac{1}{384} \left(f(\alpha)+\frac{\pi }{3}\right)^3+\frac{13 }{122880}\left(f(\alpha)+\frac{\pi }{3}\right)^5+O\left(\left(f(\alpha)+\frac{\pi }{3}\right)^7\right)$$ that is to say $$\cos(\alpha)\sim \frac{\pi }{12}+\frac{\pi ^3}{10368}+\frac{13 \pi ^5}{29859840} =0.264923$$ instead of $\cos(\alpha)=0.264932$.

Repeating the same process for the second equation around $\theta=\frac \pi 2$, using $c=\cos(\alpha)$ $$\theta=\frac \pi 2-\frac{3 \left(\frac{\pi ^3}{36}-\left(c+\frac{\pi }{6}\right)^2\right)}{6 c-2 \pi ^2+\pi }-\frac{9 \left(\frac{\pi ^3}{36}-\left(c+\frac{\pi }{6}\right)^2\right)^2 (c (6 c+\pi )+24 \pi -6)}{2 \left(6 c-2 \pi ^2+\pi \right)^3}+\cdots$$ Replacing $c$ by its approximation gives $$\theta \sim 1.62583$$

Edit

Using my favored $1,400^+$ years old approximation of the sine function $$\sin(x) \simeq \frac{16 (\pi -x) x}{5 \pi ^2-4 (\pi -x) x}\qquad (0\leq x\leq\pi)$$ let $x=2\alpha$ and we need to solve the cubic $$4 x^3+\left(16-\frac{20 \pi }{3}\right) x^2+\frac{1}{3} \pi (23 \pi -48) x-\frac{10 \pi ^3}{3}=0$$ which has only one real root $$x=\left(\frac{5 \pi }{9}-\frac{4}{3}\right)-\frac{\sqrt{\pi (48+107 \pi )-576}}{9} \times $$ $$ \sinh \left(\frac{1}{3} \sinh ^{-1}\left(\frac{13824-\pi (1728+\pi (6732+325 \pi ))}{(\pi (48+107 \pi )-576)^{3/2}}\right)\right)$$ which gives $\alpha=1.30264$.

Answer 5

I am not a mathematician but when I read R. J. Mathar's answer and some comment, I somehow found way to solve the problem.

I use the set up very similar to R. J. Mathar's answer and extend it to other possible solutions. Then I found that the all possible solutions are one of these case.

It take me many days to find answer and draw the picture since I am not expert in drawing in tikz. Here is my attempt.

Let

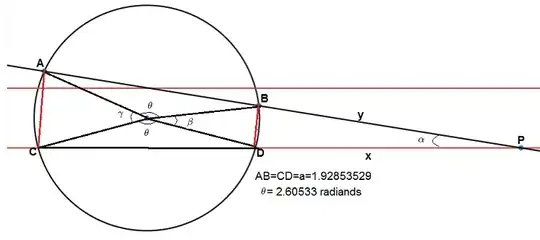
• The small black dot is Center of the circle which is at origin point $O$ (at $(0,0)$)
• Each vertex of triangle $V_0,V_1,V_2$ is at position $(x_0,y_0)$,$(x_1,y_1)$,$(x_2,y_2)$ and have angle $\theta_0,\theta_1,\theta_2$ (in radian) in order.
• Each intersect point $I_1,I_2,I_3,I_4$ is at position $(I_{1,x},I_{1,y}),(I_{2,x},I_{2,y}),(I_{3,x},I_{3,y}),(I_{4,x},I_{4,y})$ in order when $I_1$ is the intersect point at right-above and then rotate clockwise.
• $P$ is the outer perimeter of the new intersecting shape
• The red dot is Centroid of triangle $C$ which is at position $(C_x,C_y)=(\frac{x_0+x_1+x_2}{3},\frac{y_0+y_1+y_2}{3})$

Note : Only Picture 2 is in precisely approximate picture but still not actual picture. All other pictures are actual picture that use (x,y) position from the result.

$\hspace{150pt}$ Picture 1 : $x_0=0$

Picture 1 case is R. J. Mathar's answer.

From R. J. Mathar's set up, all $y_1$ and $y_2$ in every cases are always approximately equal to -0.264932. And all $I_2$ and $I_3$ in every cases are at same position.

\begin{align} x_{0,1} &= 0 \\ y_{0,1} &\approx 0.317324 \\ x_{1,1} &\approx 5.39554 \\ y_{1,1} &\approx -0.264932 \\ x_{2,1} &\approx -5.39554 \\ y_{2,1} &\approx -0.264932 \\ C_{x,1} &= 0 \\ C_{y,1} &\approx \frac{0.317324+(-0.264932)+(-0.264932)}{3} \approx -0.0708467 \\ |\overline{OC_1}|=C_{y,1} &\approx 0.0708467 \end{align}

From R. J. Mathar's answer, $t_0\approx0.181130$.

Finding all intersect point of Picture 1 ($I_{1,1},I_{2,1},I_{3,1},I_{4,1}$)

\begin{align} I_{1,x,1}=x_{0,1}+t_0(x_{1,1}-x_{0,1}) &\approx 0+0.181130(5.39554-0) \approx 0.977294 \\ I_{1,y,1}=y_{0,1}+t_0(y_{1,1}-y_{0,1}) &\approx 0.317324+0.181130((-0.264932)-0.317324) \approx 0.211860 \\ I_{2,x,1}=\sqrt{1-y_{1,1}^2} &\approx \sqrt{1-(-0.264932)^2} \approx 0.964267 \\ I_{2,y,1}=y_{1,1} &\approx -0.264932 \\ I_{3,x,1}=-I_{2,x,1} &\approx -0.964267 \\ I_{3,y,1}=I_{2,y,1} &\approx -0.264932 \\ I_{4,x,1}=-I_{1,x,1} &\approx -0.977294 \\ I_{4,y,1}=I_{1,y,1} &\approx 0.211860 \end{align}

Finding outer perimeter of Picture 1 ($P_1$)

\begin{align} P_1 =&\ |\overline{V_{1,1} I_{1,1}}| + |\overline{V_{1,1} I_{2,1}}| + (Circle\ Curve\ I_{2,1}\ to\ I_{3,1}) + |\overline{V_{2,1} I_{3,1}}| + |\overline{V_{2,1} I_{4,1}}| + (Circle\ Curve\ I_{3,1}\ to\ I_{4,1}) \\ =&\ 2(\sqrt{(x_{1,1}-I_{1,x,1})^2+(y_{1,1}-I_{1,y,1})^2} + \sqrt{(x_{1,1}-I_{2,x,1})^2+(y_{1,1}-I_{2,y,1})^2}) + 2\arcsin(I_{2,x,1}) + 2\arcsin(I_{1,x,1}) \\ \approx&\ 2(\sqrt{(5.39554-0.977294)^2+((-0.264932)-0.211860)^2} + \sqrt{(5.39554-0.964267)^2+0}) + 2\arcsin(0.964267) + 2\arcsin(0.977294) \\ \approx&\ 23.0702 \end{align}

$\hspace{150pt}$ Picture 2 : $|x_0|>0$ and $|\overline{V_0 O}|<1$

In Picture 2 and after picture, when we shift $V_0$ from the center line, the picture will lose the symmetry. Shifting to the left or right will give the similar answer but in mirror image of each other, so I will calculate only shifting to the left case.

The is the hardest one that I can't solve. I will talk about Picture 2 later in Discussion.

$\hspace{150pt}$ Picture 3 : $|\overline{V_0 O}|=1$

If we keep shifting the top vertex, at specific point we will get Picture 3 where $V_0$ and $I_4$ is the same point.

To find each value, I draw these additional lines

Because from the initial condition that each area are equal, we get

\begin{align} |\overline{V_{0,3} V_{1,3}}| &= |\overline{I_{3,3} V_{1,3}}| \\ |\overline{V_{0,3} I_{1,3}}| &= |\overline{I_{3,3} I_{2,3}}| \\ |\overline{I_{1,3} V_{1,3}}| &= |\overline{I_{2,3} V_{1,3}}| \end{align}

The triangle $V_{0,3}I_{3,3}V_{1,3}$ is isoscale triangle and line $\overline{OV_{1,3}}$ divide $\theta_{1,3}$ in to two equal angles. From this, we get

\begin{align} y_{1,3} &= y_{1,1} \approx -0.264932\\ |I_{2,x,3}| &= \sqrt{1-(y_{1,3})^2} \approx \sqrt{1-(-0.264932)^2} \approx 0.964267 \\ \frac{(Area\ V_{0,3}I_{3,3}V_{1,3})}{2} &= (Area\ OBV_{1,3}) - (Area\ OBI_{2,3}) - (Area\ ODI_{2,3}) \\ \frac{(\frac{\pi}{3})}{2} &= \frac{1}{2}|x_{1,3}||y_{1,3}| - \frac{1}{2}|I_{2,x,3}||y_{1,3}| - \pi\frac{\arctan(\frac{|x_{1,3}|}{|y_{1,3}|})-\arctan(\frac{|I_{2,x,3}|}{|y_{1,3}|})}{2\pi} \\ \frac{\pi}{6} &= \frac{0.264932}{2}|x_{1,3}| - \frac{0.264932}{2}(0.964267) - \frac{\arctan(\frac{|x_{1,3}|}{0.264932})-\arctan(\frac{0.964267}{0.264932})}{2} \\ \end{align}

This equation can be solved for $|x_{1,3}|$ analytically since there are both $|x_{1,3}|$ and $\arctan(\frac{|x_{1,3}|}{0.264932})$, so I use Wolframalpha to solve it. From picture $x_{1,3}>0$, we get

\begin{align} (Wolframalpha) \rightarrow x_{1,3} &\approx 5.75543 \\ y_{1,3} &\approx -0.264932 \\ \theta_{1,3} = 2\arctan(\frac{|x_{1,3}|}{|y_{1,3}|}) &\approx 0.0919984 \\ I_{2,x,3} = I_{2,x,1} = &\approx 0.964267 \\ I_{2,y,3} = I_{2,x,1} = &\approx -0.264932 \\ I_{3,x,3} = -I_{2,x,3} &\approx -0.964267 I_{3,y,3} = I_{2,x,1} = &\approx -0.264932 \\ I_{1,x,3} = x_{1,3} - (|x_{1,3}|-|I_{2,x,3}|)\cos(\theta_{1,3}) &\approx 0.984528 \\ I_{1,y,3} = y_{1,3} + (|x_{1,3}|-|I_{2,x,3}|)\sin(\theta_{1,3}) &\approx 0.175226 \\ x_{0,3} = x_{1,3} - (|x_{1,3}|+|I_{2,x,3}|)\cos(\theta_{1,3}) &\approx -0.935850 \\ y_{0,3} = y_{1,3} + (|x_{1,3}|+|I_{2,x,3}|)\sin(\theta_{1,3}) &\approx 0.352398 \\ \end{align}

Finding $x_{2,3}$

\begin{align} (Angle\ \widehat{I_{3,3}OV_{0,3}}) &= 2\pi - 4\arctan(\frac{|I_{2,x,3}|}{|y_{1,3}|}) - 2\left(\arctan(\frac{|x_{1,3}|}{|y_{1,3}|})-\arctan(\frac{|I_{2,x,3}|}{|y_{1,3}|})\right) \\ &\approx 0.628265 \\ (Chord\ Area\ I_{3,3}V_{0,3}) &= \frac{(Angle\ \widehat{I_{3,3}OV_{0,3}})-sin(Angle\ \widehat{I_{3,3}OV_{0,3}})}{2}\\ &\approx 0.0202615 \\ (Area\ I_{3,3}V_{2,3}V_{0,3}) &= (Area\ Triangle\ I_{3,3}V_{2,3}V_{0,3}) - (Chord\ Area\ I_{3,3}V_{0,3}) \\ \frac{\pi}{3} &= \frac{1}{2}(|x_{2,3}|-|I_{3,x,3}|)(|y_{0,3}|+|y_{1,3}|) - (Chord\ Area\ I_{3,3}V_{0,3}) \\ \frac{\pi}{3} &\approx \frac{1}{2}(|x_{2,3}|-0.964267)(0.352398+0.264932) - 0.0202615 \\ |x_{2,3}| &\approx 4.42258 \\ (x_{2,3}<0) \rightarrow x_{2,3} &\approx -4.42258 \\ y_{2,3} &\approx -0.264932 \\ \end{align}

Finding centroid ($C_3$)

\begin{align} C_{x,3} = \frac{x_{0,3}+x_{1,3}+x_{2,3}}{3} &\approx 0.132333 \\ C_{y,3} = \frac{y_{0,3}+y_{1,3}+y_{2,3}}{3} &\approx -0.059155 \\ |\overline{OC_3}|=\sqrt{C_{x,3}^2+C_{y,3}^2} &\approx 0.144950 \end{align}

Finding outer perimeter ($P_3$)

\begin{align} P_3 =&\ |\overline{V_{2,3} V_{0,3}}| + |\overline{V_{2,3} I_{3,3}}| + 2|\overline{I_{2,3} V_{1,3}}| + 2(Circle\ Curve\ I_{2,3}\ to\ I_{3,3})\\ =&\ \sqrt{(x_{2,3}-x_{0,3})^2+(y_{2,3}-y_{0,3})^2} + |x_{2,3}-I_{3,x,3}| + 2|I_{2,x,3}-x_{1,3}| + 2(2\arcsin(I_{2,x,3}))\\ \approx&\ 21.7922 \end{align}

$\hspace{150pt}$ Picture 4 : $|\overline{V_0 O}|>1$ and $|\overline{V_0 V_1}|<|\overline{V_2 V_1}|$

In Picture 4, $V_{1,4},I_{1,4},I_{2,4},I_{3,4},I_{4,4},$ are the same point as in Picture 3, so

\begin{align} x_{1,4} &\approx 5.75543 \\ y_{1,4} &\approx -0.264932 \\ I_{1,x,4} &\approx 0.984528 \\ I_{1,y,4} &\approx 0.175226 \\ I_{2,x,4} &\approx 0.964267 \\ I_{2,y,4} &\approx -0.264932 \\ I_{3,x,4} &\approx -0.964267 \\ I_{3,y,4} &\approx -0.264932 \\ I_{4,x,4}=x_{0,3} &\approx -0.935850 \\ I_{4,y,4}=y_{0,3} &\approx 0.352398 \\ \theta_{1,4}=\theta_{1,3} &\approx 0.0919984 \\ y_{2,4}= y_{1,4} &\approx -0.264932 \end{align}

There are infinite solutions for Picture 4 where $x_{2,3}<x_{2,4}<x_{2,5}$. In Picture 4, I use $x_{2,4}=\frac{x_{2,3}+x_{2,5}}{2}$

Finding relation between $x_{2,4}$ and $x_{0,4},y_{0,4}$

\begin{align} |\overline{V_{0,4}V_{1,4}}| &= |\overline{V_{0,4}I_{4,4}}| + |\overline{I_{4,4}V_{1,4}}|\\ &= |\overline{V_{0,4}I_{4,4}}| + |\overline{I_{3,4}V_{1,4}}|\\ &= \left(\frac{|x_{0,4}|-|I_{4,x,4}|}{cos(\theta_{1,4})}\right) + (|I_{3,x,4}|+|x_{1,4}|)\\ (Area\ Triangle\ V_{0,4}V_{1,4}V_{2,4}) &= \frac{1}{2}|\overline{V_{2,4}V_{1,4}}||\overline{V_{0,4}V_{1,4}}|sin(\theta_{1,4}) \\ \pi &= \frac{sin(\theta_{1,4})}{2}(|x_{2,4}|+|x_{1,4}|)\left(\left(\frac{|x_{0,4}|-|I_{4,x,4}|}{cos(\theta_{1,4})}\right) + (|I_{3,x,4}|+|x_{1,4}|)\right) \\ \frac{2\pi}{sin(0.0919984)} &\approx (|x_{2,4}|+|5.75543|)\left(\left(\frac{|x_{0,4}|-|-0.935850|}{cos(0.0919984)}\right) + (|-0.964267|+|5.75543|)\right) \\ |x_{0,4}| &\approx \frac{34.9789 - 5.75543|x_{2,4}|}{|x_{2,4}|+5.75543} \\ (Area\ Triangle\ V_{0,4}V_{1,4}V_{2,4}) &= \frac{1}{2}(Base\ Length)(Height\ Length) \\ \pi &= \frac{1}{2}|\overline{V_{2,4}V_{1,4}}|(|y_{0,4}|+|y_{1,4}|) \\ 2\pi &= (|x_{2,4}|+|x_{1,4}|)(|y_{0,4}|+|y_{1,4}|) \\ 2\pi &\approx (|x_{2,4}|+|5.75543|)(|y_{0,4}|+|-0.264932|) \\ |y_{0,4}| &\approx \frac{2\pi}{|x_{2,4}|+5.75543}-0.264932 \\ \end{align}

From Picture 4, $x_{0,4},x_{2,4}<0$ and $y_{0,4}>0$

\begin{align} x_{0,4} &\approx -\frac{5.75543x_{2,4} + 34.9789}{5.75543-x_{2,4}} \\ y_{0,4} &\approx \frac{2\pi}{5.75543-x_{2,4}}-0.264932 \\ \end{align}

Finding centroid ($C_4$) when $x_{2,3}<x_{2,4}<x_{2,5}$

\begin{align} C_{x,4} &= \frac{x_{0,4}+x_{1,4}+x_{2,4}}{3} \\ &\approx \frac{-\frac{5.75543x_{2,4} + 34.9789}{5.75543-x_{2,4}}+5.75543+x_{2,4}}{3} \\ &\approx \frac{x_{2,4}^2+5.75543x_{2,4}+1.85401}{3(x_{2,4}-5.75543)} \\ C_{y,4} &= \frac{y_{0,4}+y_{1,4}+y_{2,4}}{3} \\ &\approx \frac{\left(\frac{2\pi}{5.75543-x_{2,4}}-0.264932\right)+(-0.264932)+(-0.264932)}{3} \\ &\approx \frac{0.264932x_{2,4}+0.569598}{5.75543-x_{2,4}} \\ |\overline{OC_4}| &= \sqrt{C_{x,4}^2+C_{y,4}^2} \\ &\approx \sqrt{\left(\frac{x_{2,4}^2+5.75543x_{2,4}+1.85401}{3(x_{2,4}-5.75543)}\right)^2+\left(\frac{0.264932x_{2,4}+0.569598}{5.75543-x_{2,4}}\right)^2} \\ &\approx \frac{\sqrt{x_{2,4}^4+11.5109x_{2,4}^3+37.4645x_{2,4}^2+24.0565x_{2,4}+6.35702}}{3(5.75543-x_{2,4})} \end{align}

Finding outer perimeter ($P_4$)

\begin{align} 2|\overline{I_{2,4} V_{1,4}}| + 2(Circle\ Curve\ I_{2,4}\ to\ I_{3,4}) =&\ 2|I_{2,x,4}-x_{1,4}| + 2(2\arcsin(I_{2,x,4}))\\ \approx&\ 14.7930 \end{align} \begin{align} P_4 =&\ |\overline{V_{2,4} V_{0,4}}| + |\overline{I_{4,4} V_{0,4}}| + |\overline{V_{2,4} I_{3,4}}| + 2|\overline{I_{2,4} V_{1,4}}| + 2(Circle\ Curve\ I_{2,4}\ to\ I_{3,4})\\ =&\ \sqrt{(x_{2,4}-x_{0,4})^2+(y_{2,4}-y_{0,4})^2} + \sqrt{(I_{4,x,4}-x_{0,4})^2+(I_{4,y,4}-y_{0,4})^2} + |x_{2,4}-I_{3,x,4}| + 14.7930 \\ =&\ \sqrt{\left(x_{2,4}-\left(-\frac{5.75543x_{2,4} + 34.9789}{5.75543-x_{2,4}}\right)\right)^2+\left((-0.264932)-\left(\frac{2\pi}{5.75543-x_{2,4}}-0.264932\right)\right)^2} + \sqrt{\left((-0.935850)-\left(-\frac{5.75543x_{2,4} + 34.9789}{5.75543-x_{2,4}}\right)\right)^2+\left(0.352398-\left(\frac{2\pi}{5.75543-x_{2,4}}-0.264932\right)\right)^2} + ((-0.964267)-x_{2,4}) + 14.7930 \\ \approx&\ \frac{\sqrt{x_{2,4}^4 - 23.0217 x_{2,4}^3 + 62.5421 x_{2,4}^2 + 805.274 x_{2,4} + 1263.00}+\sqrt{45.1543 x_{2,4}^2 + 399.397 x_{2,4} + 883.181}}{5.75543-x_{2,4}}+13.8287-x_{2,4} \end{align}

I will explain about these centroid ($C_4$) function and outer perimeter ($P_4$) function more in Discussion.

$\hspace{150pt}$ Picture 5 : $|\overline{V_0 V_1}|=|\overline{V_2 V_1}|$

Picture 5 is the special case of Picture 4 when |\overline{V_0,5 V_1,5}|=|\overline{V_2,5 V_1,5}|.

If we move $x_{2,5}$ to the right more, we will get the mirror image of Picture 4.

From Picture 4, we get

\begin{align} x_{1,5} &\approx 5.75543 \\ y_{1,5} &\approx -0.264932 \\ I_{1,x,5} &\approx 0.984528 \\ I_{1,y,5} &\approx 0.175226 \\ I_{2,x,5} &\approx 0.964267 \\ I_{2,y,5} &\approx -0.264932 \\ I_{3,x,5} &\approx -0.964267 \\ I_{3,y,5} &\approx -0.264932 \\ I_{4,x,5} &\approx -0.935850 \\ I_{4,y,5} &\approx 0.352398 \\ \theta_{1,5} &\approx 0.0919984 \\ y_{2,5}= y_{1,5} &\approx -0.264932 \end{align}

Finding $x_{2,5}$ when $x_{2,5}<0$

\begin{align} (Area\ Triangle\ V_{0,5}V_{1,5}V_{2,5}) &= \frac{1}{2}|\overline{V_{2,5}V_{1,5}}||\overline{V_{0,5}V_{1,5}}|sin(\theta_{1,5}) \\ 2\pi &= (|x_{2,5}|+|x_{1,5}|)^2sin(\theta_{1,5}) \\ \frac{2\pi}{sin(0.0919984)} &\approx (|x_{2,5}|+5.75543)^2 \\ x_{2,5} &\approx -2.51458 \end{align}

We can use the formula of $x_{0,4},y_{0,4},C_{x,4},C_{y,4},|\overline{OC_4}|,P_4$ from Picture 4 to calculate those value for Picture 5. But I will calculate those value with geometry instead and use the value I get to check if those formula are correct or not.

\begin{align} x_{0,5} = x_{1,5} - (|x_{1,5}|+|x_{2,5}|)\cos(\theta_{1,5}) &\approx -2.47961 \\ y_{0,5} = y_{1,5} + (|x_{1,5}|+|x_{2,5}|)\sin(\theta_{1,5}) &\approx 0.494823 \\ C_{x,5}= \frac{x_{0,5}+x_{1,5}+x_{2,5}}{3} &\approx 0.253748 \\ C_{y,5}= \frac{y_{0,5}+y_{1,5}+y_{2,5}}{3} &\approx -0.011680 \\ |\overline{OC_5}|=\sqrt{C_{x,5}^2+C_{y,5}^2} &\approx 0.254017 \end{align} \begin{align} 2|\overline{I_{2,5} V_{1,5}}| + 2(Circle\ Curve\ I_{2,5}\ to\ I_{3,5}) =&\ 2|I_{2,x,5}-x_{1,5}| + 2(2\arcsin(I_{2,x,5}))\\ \approx&\ 14.7930 \end{align} \begin{align} P_5 &= |\overline{V_{2,5} V_{0,5}}| + 2|\overline{V_{2,5} I_{3,5}}| + 2|\overline{I_{2,5} V_{1,5}}| + 2(Circle\ Curve\ I_{2,5}\ to\ I_{3,5}) \\ &= \sqrt{(x_{2,5}-x_{0,5})^2+(y_{2,5}-y_{0,5})^2} + 2|x_{2,5} - I_{3,x,5}| + 14.7930 \\ &\approx 18.6542 \\ \end{align}

When I can use the formula of $x_{0,4},y_{0,4},C_{x,4},C_{y,4},|\overline{OC_4}|,P_4$ from Picture 4 to calculate those value, all of they also give the same value. So, the formula is correct.

$\hspace{150pt}$ Discussion and conclusion

Let start with Picture 2. I think it is possible to calculate each value in Picture 2 at specific $x_{0,2}$ numerically with R. J. Mathar's method. Because of that, I think it is impossible find analytic function of the relation between $x_{0,2}$ and $|\overline{OC_2}|,P_2$ like what I find for Picture 4.

I think it is possbile to find the approximate function in form of series expansion but that is beyond my knowledge, sorry.

As Picture 2 is transition phase between Picture 1 and Picture 3, we can assume that

\begin{align} x_{0,3}<x_{0,2}<x_{0,1} &\rightarrow -0.935850<x_{0,2}<0 \\ y_{0,1}<y_{0,2}<y_{0,3} &\rightarrow 0.317324<y_{0,2}<0.352398 \\ x_{1,1}<x_{1,2}<x_{1,3} &\rightarrow 5.39554<x_{1,2}<5.75543 \\ y_{1,2}=y_{1,1} &\approx -0.264932 \\ x_{2,1}<x_{2,2}<x_{2,3} &\rightarrow -5.39554<x_{2,2}<-4.42258 \\ y_{2,2}=y_{2,1} &\approx -0.264932 \end{align}

Note : In Picture, I just use $x_{a,2}=\frac{x_{a,1}+x_{a,3}}{2}$ and $y_{a,2}=\frac{y_{a,1}+y_{a,3}}{2}$ when $a=0,1,2$ so all 5 areas aren't complete equal.

With those upper and lower limit, it is still impossible to tell if $|\overline{OC_1}|<|\overline{OC_2}|<|\overline{OC_3}|$ and $P_3<P_2<P_1$ without additional condition which I can't find and proof what they are exactly.

However, I can use the value I get to plot in https://www.desmos.com/calculator

$\hspace{150pt}$ Let start with centroid (C)

Desmos code

(0,0)
x^2+y^2=1
y = (-2.22343*10^{12} x^2 - 1.45103*10^{14} (7.5*10^{9} x^2 - 8.63314*10^{10} x + 2.1424*10^{10})^{0.5} - 1.25663*10^{19} x + 1.53371*10^{17})/(8.3925*10^{12} x^2 - 9.66048*10^{13} x + 2.72416*10^{20})
(0,-0.0708467)
(0.132333,-0.059155)
(0.219683,-0.037873)
(0.253748,-0.011680)

From the graph

• x axis is $C_x$
• y axis is $C_y$
• The radius of circle is 1.
• Black dot is $C_1$
• Red dot is $C_3$
• Blue dot is $C_4$
• Green dot is $C_5$
• Purple graph is postion centroid from $C_4$ formula that we get which is qualify for $0.132333<C_x<0.253748$.

I try to fit those dot with ellipse. It fit pretty well but not fit exactly.

Desmos code

(0,0)
x^2/(0.240477)^2+y^2/(0.0708467)^2=1
x^2/(0.259943)^2+y^2/(0.0708467)^2=1
x^2/(0.257268)^2+y^2/(0.0708467)^2=1
y = (-2.22343*10^{12} x^2 - 1.45103*10^{14} (7.5*10^{9} x^2 - 8.63314*10^{10} x + 2.1424*10^{10})^{0.5} - 1.25663*10^{19} x + 1.53371*10^{17})/(8.3925*10^{12} x^2 - 9.66048*10^{13} x + 2.72416*10^{20})
(0,-0.0708467)
(0.132333,-0.059155)
(0.219683,-0.037873)
(0.253748,-0.011680)

From the graph

• x axis is $C_x$
• y axis is $C_y$
• The radius of circle is 1.
• Red dot is $C_1$
• Blue dot is $C_3$
• Green dot is $C_4$
• Purple dot is $C_5$
• Black graph is postion centroid from $C_4$ formula that we get which is qualify for $0.132333<C_x<0.253748$.
• Blue ellipse pass $C_1$ and $C_3$
• Green ellipse pass $C_1$ and $C_4$
• Purple ellipse pass $C_1$ and $C_5$

Here is a graph between $x_2$ and $|\overline{OC}|$

The scale of x axis and y axis is same, so we don't see much thing in Desmos in this case.

So, I use Wolframalpha to plot instead.

From left to Right, each dot are $|\overline{OC_1}|,|\overline{OC_3}|,|\overline{OC_4}|,|\overline{OC_5}|$

Here is a graph between $x_{2,4}$ and $|\overline{OC_4}|$ in range $x_{2,4}<x_{2,4}<I_{3,x,4}$ or $-4.42258<x_{2,4}<-0.964267$

Note : The formula of $|\overline{OC_4}|$ that we get still work in range $x_{2,5}<x_{2,4}<I_{3,x,4}$ or $-2.51458<x_{2,4}<-0.964267$

The maximum |\overline{OC_4}| is at $x_{2,4}=x_{2,5}$. So, $|\overline{OC_4}|\le|\overline{OC_5}|$

From all graph, it is very like that "the longest possible the distance from the center of the circle to the centroid of the triangle" $=|\overline{OC_5}|\approx0.254017$

For "the shortest possible the distance from the center of the circle to the centroid of the triangle", the value might be equalt to $|\overline{OC_1}|\approx0.0708467$ or slightly less than that in some case of Picture 2 that is very close to Picture 1.

$\hspace{150pt}$ About outer parimeter ($P$)

Here is a graph between $x_2$ and $P$

From left to Right, each dot are $P_1,P_3,P_4,P_5$

From the formula of $P_4$ we get, here is a graph between $x_{2,4}$ and $P_4$ in range $-4.42258<x_{2,4}<-0.964267$

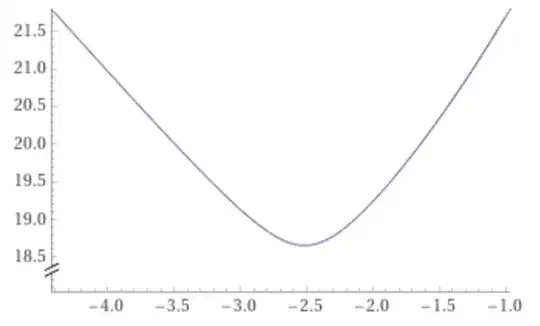
The minimum $P_4$ is at $x_{2,4}=x_{2,5}$. So, $P_4\ge P_5$

From all graph of $P$, it is very like that "the shortest possible length of outer perimeter of new intersecting shape" $=P_5\approx18.6542$

For "the longest possible length of outer perimeter of new intersecting shape", the value might be equalt to $P_1\approx23.0702$ or slightly more than that in some case of Picture 2 that is very close to Picture 1.