After thinking about this for a very long time, I think I may finally have an answer:
We start with the two-sphere $\mathcal{S}^2$ equipped with the (length-invariant) metric:
$$ds^2 = d\theta^2 + \sin^2 \theta d\phi^2$$
where $\theta = 0$ is the north pole, $\theta = \pi/2$ is the equator and $\theta=\pi$ is the south pole. This further means that:
- $g_{\theta \theta} = 1$
- $g_{\phi \phi} = \sin^2\theta$
- $g_{\theta \phi} = g_{\phi \theta} = 0$
There are infinitely many connections we can consider, but we will focus on three desirable properties:
- Metric Compatibility
- Zero Torsion
- Zero Curvature
For now Zero Torsion, means the ability of the quadrilateral to "close" which can be expressed as:
$$\nabla_{\theta} \partial_\phi = \nabla_{\phi} \partial_\theta $$
or equivalently as:
$$\Gamma_{\theta \phi}^k = \Gamma_{\phi \theta}^k \text{ for } k = \theta, \phi$$
Geometrically, this is the imposing of the most natural symmetry on the way we connect the fibers (leveraging an extra degree of freedom). More on that later.
It is instructive to see how the choices of the connection coefficients (Christoffel symbols) are affected as we are imposing any of these restrictions. It is also interesting to see how we can never get all three to work on $\mathcal{S}^2$.
For example, if we wanted to impose Metric Compatibility, then the covariant derivative of the metric should be zero in any direction. This has several consequences. For starters:
$\nabla_{\theta} g_{\phi \phi} = 0 \Rightarrow 2\sin\theta\cos\theta - \Gamma_{\theta \phi}^k g_{k \phi} - \Gamma_{\theta \phi}^k g_{\phi k} = 0 \Rightarrow \sin\theta\cos\theta = \Gamma_{\theta \phi}^k g_{k \phi} = \Gamma_{\theta \phi}^{\phi} g_{\phi \phi} = \Gamma_{\theta \phi}^{\phi} \sin^2\theta$
where we used the definition of the metric above. This yields:
$$\boxed{\Gamma_{\theta \phi}^{\phi} = \cot\theta}$$
This is already very informative! On the one hand, we already know that our metric preserves lengths on $\mathcal{S}^2$, thus any Metric Compatible connection can only rotate the basis vectors of the Fibers and thus the Fibers themselves (no stretching, shearing, or reflections).
We can also see this numerically: As we move North our default measure sticks shrink, so if we want no size distortions in our map, we should adjust our horizontal "measure sticks" (horizontally) as we are moving vertically. This is what the term $\Gamma_{\theta \phi}^{\phi} = \cot\theta $ does.
If we instead simply let all $\Gamma_{ij}^k = 0$ - including $\Gamma_{\theta \phi}^{\phi} = 0$), we end up with something like the Mercator projection, which is certainly NOT an isometric projection, as it gets highly distorted (horizontally stretched) near the poles. Let's call this Mercator-like connection, the "Distorted Connection". The Distorted Connection (which is only defined on $\mathcal{S}^2$ with its poles removed), is flat and torsion-less but incompatible with the metric:

Let's continue our calculations assuming metric compatibility. This time consider:
$\nabla_{\phi} g_{\theta \phi} = 0 \Rightarrow 0 - \Gamma_{\phi \theta}^k g_{k \phi} - \Gamma_{\phi \phi}^l g_{\theta l} = 0 \Rightarrow \Gamma_{\phi \theta}^{\phi} g_{\phi \phi} + \Gamma_{\phi \phi}^{\theta} g_{\theta \theta} = 0 \Rightarrow \Gamma_{\phi \theta}^{\phi} \sin^2\theta + \Gamma_{\phi \phi}^{\theta} = 0$
where we again used the definition of the metric. This time around we do not have a unique solution, since we have two coefficients and one equation, namely:
$$ \boxed{\Gamma_{\phi \phi}^{\theta} = -\Gamma_{\phi \theta}^{\phi} \sin^2\theta} $$
This is where the extra degree of freedom comes in! A "sensible" choice would be to set $\Gamma_{\phi \theta}^{\phi} = \Gamma_{\theta \phi}^{\phi} = \cot\theta$ in which case we can also get:
$$\boxed{\Gamma_{\phi \phi}^{\theta} = -\sin\theta\cos\theta}$$
This is of course the Levi-Civita connection (once we set all other coefficients equal be zero).
Why is this "sensible"? For starters due to Metric Compatibility, our Fibers (Tangent Spaces) are again rotating. However we get more than that. The Fibers rotate in a compatible way, in the sense that the corners of their Grids seem to overlap locally.
This is what Zero Torsion does to the Fibers, and what quadrilateral closing looks locally.
(Formally, this is the best linear approximation or Taylor's expansion up to linear terms - which means there will be $O(\epsilon^2)$ errors - but for intuition purposes it suffices to imagine locally wrapping each $T_pM$ around $p$ on $M$). A picture is probably best to express this:
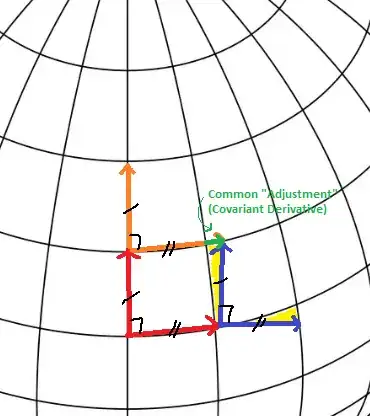
Notice that as we move North (red to orange), Metric Compatibility forces us to extend the horizontal "measuring stick" beyond where we would expect it to be based on our charting. This is to make sure that all frames look identical (up to rotation). To keep this new gridding consistent, we have to rotate our frame as we are moving East to compensate (red to blue).
This necessary "rotation of the squares" (ie. $\Gamma_{\phi \phi}^{\theta} \neq 0$ which means that transporting the $\partial_{\phi}$ basis vector in the "horizontal" $\partial_{\phi}$ direction picks up a shift in the the "vertical" $\partial_{\theta}$ direction, thus rotating $\partial_{\phi}$) is essentially what leads to non-zero curvature.
But what if we chose something less sensible, but nevertheless allowable? For instance what if we instead chose:
$$\boxed{\Gamma_{\phi \phi}^{\theta} = \Gamma_{\phi \theta}^{\phi} = 0} $$
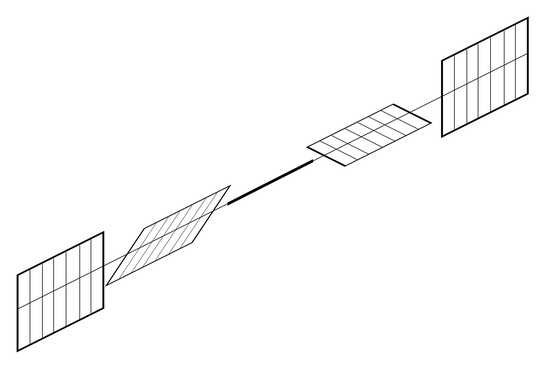
This time there is no rotation of "adjacent" Fibers, thus there is no curvature. But there is something very sneaky. Unlike before, local consistent "gridding" is NOT possible! This is because there is no longer a well defined quadrilateral.
The quadrilateral does not "close" to define proper gridding! Let's call this the Torsion Connection. Of course we can still draw our frames but there will be either "gaps" or "overlaps" (Here we have overlaps):

This is exactly what the fibers tell us about the torsion:
Torsion measures the infinitesimal misalignment of squares (hyper-rectangles) of nearby Fibers.
(This can be made precise using Taylor approximations but we already have precise definitions of Torsion. What I am interested is a "quick and dirty" geometric intuition).
Interestingly enough, like the Distorted Connection, the Torsion Connection is also (locally) flat, because the angle of a vector with the latitude never changes during parallel transport. What is different is that the latter is metric compatible while the former is not. On the flip side, the former is torsion-free ("Gridable") where the latter is not.
This answers another question:
In the absence of curvature, $\phi_{\gamma}$ is always equal to the
identity regardless of whether we have metric compatibility or torsion
(or anything in between).
For length preserving metrics we can check for Metric Compatibility by looking for (absence of) distortions of frames. For generic metrics we should only allow linear transformations on the Fibers that preserve the metric. This can be done formally and intrinsically by making sure the covariant derivative of the metric is zero in all directions.
And we can check for torsion by checking for overlaps of "frame squares" in $M$ (formally by making sure that $\Gamma_{ij}^k = \Gamma_{ji}^k$).
SUMMARY:
Of the three properties above (Metric Compatibility, Torsion-less and Zero Curvature) we can ONLY make two of them to work on $\mathcal{S}^2$ (Locally. Only Levi-Civita is global). No matter how hard we try, at least one of these properties will fail. Colloquially speaking this is because, in some sense, $\mathcal{S}^2$ has intrinsic curvature, so in order to make it (locally) flat, we need to "cheat" in some way. Specifically:
- The Levi-Civita Connection has Curvature (Fibers rotate compatibly).
- The Distorted Connection is Metric InCompatible (Fibers Stretch).
- The Torsion Connection has Torsion (Fibers rotate incompatibly).