Solving Special Case of Cubic Equation

Question

Given a cubic equation of standard form $ax^3 + bx^2 + cx + d = 0$ where $a, b, c, d$ are real numbers, if we know that there is only one real root $x_r$, we know $x_r>0$, and we only care about finding $x_r$ (ie. we don't care about solving for the other two roots), is there an easier/better way to find that single root than using the Cardano method or some numerical approximation?

Thanks!

Edit: For clarity, looking for an equation for $x_r$ in terms of the coefficients, by "easier" I mean smallest number of operations but can be in a sequence of functions or trigonometric, essentially looking for anything that has fewer operations than Cardano

Answer 1

If you are looking for roots of a cubic equation having real coefficients $a$, $b$, $c$, and $d$ in form of an equation or some mathematical expression, then you have to resort to using the formulae of Cardano and Vieta. @ClaudeLeibovici has already answered your question using that method. Here is another way to calculate only the sought real root of a cubic equation using an expression containing radicals.

Assuming $a\neq 0$, we divide the given cubic equation by $a$ to obtain, $$x^3+\beta x^2+\gamma x+\delta=0.$$

First we calculate two quantities $m$ and $n$ as shown below. They are supposed to facilitate the presentation of our solution. $$m=\dfrac{\gamma}{3}-\dfrac{\beta^2}{9}$$ $$n=\dfrac{\beta^3}{27}-\dfrac{\beta\gamma}{6}+\dfrac{\delta}{2}$$

If you examine the expressions given for $m$ and $n$, you will notice that $m=\dfrac{p}{3}$ and $n=\dfrac{q}{2}$, where $p$ and $q$ are defined in @ClaudeLeibovici’s answer.

Now, we are in a position to write down the equation for the one and only real root as a function of $m$ and $n$. $$x_\text{real root}=\sqrt[3]{-n+\sqrt{n^2+m^3}}-\sqrt[3]{n+\sqrt{n^2+m^3}}-\dfrac{\beta}{3}$$

Answer 2

There is a much better method to solve the cubic equation $$ax^3 + bx^2 + cx + d = 0$$ To simplify, assuming $a\neq 0$, divide all coefficients by $a$ and consider $$x^3+\beta x^2+\gamma x +\delta=0$$ Define $$p=\gamma -\frac{\beta ^2}{3}\qquad \text{and}\qquad q=\frac{2 \beta ^3}{27}-\frac{\beta \gamma }{3}+\delta$$and, using the hyperbolic method for one real root $$\color{blue}{x_r=-2\frac{|q|}{q}\sqrt{-\frac{p}{3}}\cosh\left[\frac{1}{3}\operatorname{arcosh}\left(\frac{-3|q|}{2p}\sqrt{\frac{-3}{p}}\right)\right]-\frac \beta 3}\qquad \color{red}{\text{if}\qquad p <0}$$ $$\color{blue}{x_r= -2\sqrt{\frac{p}{3}}\sinh\left[\frac{1}{3}\operatorname{arsinh}\left(\frac{3q}{2p}\sqrt{\frac{3}{p}}\right)\right]-\frac \beta 3}\qquad \color{red}{\text{if}\qquad p >0}$$

Answer 3

If elementary differential calculus can be used we can take help of graph of cubic to obtain a single real root $x_r$.

The graph appears like a rocket course that initially begins to plummet for $a>0$ but recovers to rise again. ( For $a<0$ the order is reversed with first plummet, rise and plummet again).

In doing so the graph should keep $(y_{max}/y_{min})$ both above or both below the x-axis with a single intersection at $x_r$, so that their product is positive.

The constant coefficient $d$ influences by entire cubic graph $y$ shifting up or down, so I have included here elementary min/max differential calculus.

$$ y(x)=ax^4+bx^2+cx+d \tag 1$$

Its graph should cut x-axis only once. Maximum/minimum values $y(x_1), y(x_2)$ at roots $(x_1,x_2)$ of parabola are found by differentiation.

$$ \frac{dy(x)}{dx}=3ax^2+2bx+c=0 $$

$$(x_1,x_2)= \left(\frac{-b+\sqrt{b^2-3ac }}{3a},\frac{-b-\sqrt{b^2-3ac}}{3a}\right) $$

The clue to find determinant for single intersection $x_r$ of graph is when extrema are on same side of x-axis ( here red and green ), i.e., discriminant for single $x_r$

$$ \Delta= y(x_1)\cdot y(x_2)>0$$

For three intersections/real roots the discriminant $$ \Delta<0$$

and for a single root and a double root that has tangential contact with x-axis we have

$$ \Delta=0$$

By simplification we find the discriminant

$$\boxed{\Delta=\frac{a(4c^3+27ad^2)+b(4b^2d -bc^2-18acd)}{27 a^2}}$$

It can be derived with Cardano formulae but believe it would be more cumbersome to go around and express it in terms of given $(a,b,c,d)$.

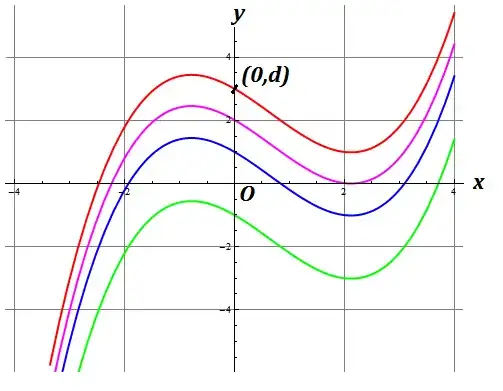
Plots generated for cubic coefficients $(a,b,c)=(.2,-0.4,-1)$, $d =(3,\approx 2.01213,1,-1)$ for four cubics shown above.

A a unique single root/ numerical solution of (1) can be obtained subject to condition $\Delta>0 $ satisfied by given coefficients