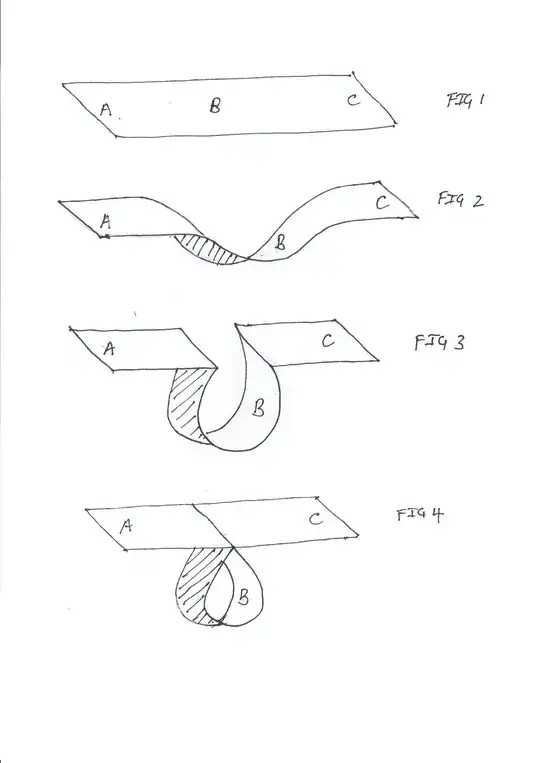
Imagine there is a 2-d plane as in Fig 1. I know nobody can live on a 2-d plane, but imagine a Flatlander standing (if that's what Flatlanders do) at position A. The Flatlander can then move through position B to position C.
If we then give the 2-d plane a little extrinsic curvature, as in Fig 2 (the cross-hatching is meant to indicate the underside of the plane - I apologize for my lack of drawing talent), the Flatlander can still move from A to C, through B, and shouldn't notice any difference from Fig 1.
In Fig 3, the extrinsic curvature is a little more severe, and there are a couple of folds in the 2-d plane (can 2-d planes have folds?). The Flatlander should still be able to move from point A, through B, to point C.
In Fig 4 though, the "folds" in Fig 3 have been brought together, and the "join" is smooth, so the part of the plane that includes point B has been "pinched-off" from the parts that contain points A and C.
My questions are:
(a) In Fig 3, what does the Flatlander see (assuming Flatlanders can see) as they move from point A to point B, especially when they approach the "fold"? Presumably they can see point B and point C as though Flatland is still flat - is there any noticeable effect at the "folds"?
(b) in Fig 4 the single "join" is smooth and complete - I assume the Flatlander standing at point A looks along Flatland and sees point C, but cannot see point B (so Flatland is a little shorter than it used to be). Furthermore, I assume the Flatlander cannot access the segment of Flatland that contains point B. Are my assumptions here correct, and of not, why not?