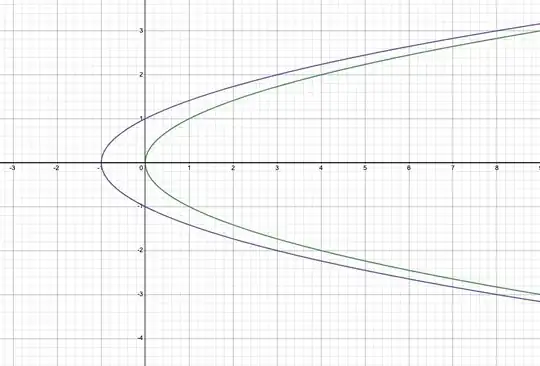
I read here that the shortest distance between two differentiable non-intersecting curves is along their common normal.
But if we consider $y^2=x+1$, $y^2 = x$, their common normal is actually the largest possible distance:
Maybe this is because the minimum distance between these two curves never exists in the first place... Is this a condition we should add in the statement?
Thanks