5

We were taught a geometrical proof of the identity $\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$ which consisted of drawing a triangle in a rectangle and looked like this:-
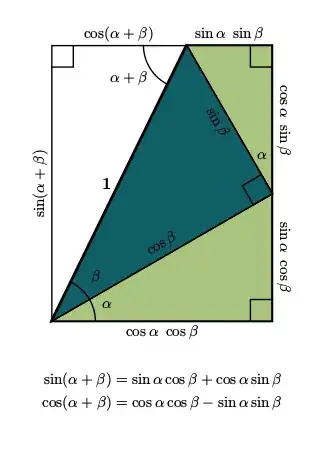
enter image description here


While I have no problem understanding this proof as long as the sum of the angles is an acute angle, I am not able to visualize how this proof works if the sum of the angles is not an acute angle. How would this proof work if one angle is $120^\circ$ while the other is $285^\circ$ or $195^\circ$?

J.G.
  • 115,835
Pumpkin_Star
  • 193
  • Woo-hoo! That's my diagram ... slightly tweaked and weirdly re-tinted by plagiarists, but mine nonetheless! :) ... Anyway, here's a follow-up answer that discusses adapting the figure to a couple of obtuse cases. If it sufficiently addresses your needs, then perhaps this question should be closed as a duplicate. – Blue Aug 15 '22 at 12:02
  • @Blue I think this may come from https://web.ma.utexas.edu/users/m408n/CurrentWeb/LM0-5-5.php. You could ask where they got it. There's also https://www.cut-the-knot.org/triangle/SinCosFormula2.shtml, without the colors, citing a book from 2000. – David K Aug 28 '22 at 23:58
  • @Blue One of the figures at https://trigonometric-formulas.blogspot.com/2016/11/angle-sum-and-difference-identities.html looks even more like yours, including the enlarged $1$ and the color scheme. – David K Aug 29 '22 at 00:07
  • @DavidK: I believe the Cut-the-Knot images (via Nelson's Proofs without Words, II) arise from "parallel evolution"; there are common variants of those, too, including ones embedded in the Unit Circle. Distinctive aspects of my figure that I like (and have been advocating since well before 2000) are reduced visual clutter by eliminating overlapping elements, and color-matching the similar sub-triangles. Of course, I don't claim to be the first person in history to concoct "my" figure ... but it seems pretty clear that my particular rendition has (in)directly "inspired" others. Yay, me! :) – Blue Aug 29 '22 at 03:32
  • I came up with what I believe is an all-angles proof in a single diagram, although not quite as pretty and obvious as the one in the question. That diagram is also an answer to the much earlier (and more general) question, How can I understand and prove the "sum and difference formulas" in trigonometry? Because an answer should be posted only once, I've posted my answer under the older question. Here it is, if you're interested. – David K Aug 30 '22 at 00:17

1 Answers1

2

See picture below. Note that angle $\beta$ is in fourth quadrant, that's why $BC=-\sin\beta$.

enter image description here

Ivan Kaznacheyeu
  • 4,188