Looking at the polynomial $f\left(x\right)=x^{3}-2 $ over $\mathbb{Q}$, and with $ \rho=\sqrt[3]{2}, \zeta = \zeta_{3} $ (3'rd unit root).
The roots of $ f $ are $ \left(\rho,\rho\zeta_{3},\rho\zeta_{3}^{2}\right) $, So $ \mathbb{E}=\mathbb{Q}\left(\rho,\rho\zeta_{3},\rho\zeta_{3}^{2}\right)=\mathbb{Q}\left(\rho,\zeta_{3}\right) $ is the splitting field of $ f $ over $ \mathbb{Q} $.
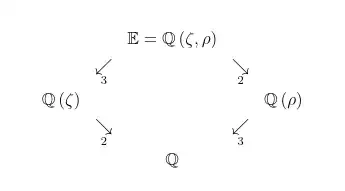
Now I saw the following diagram regarding this problem, which made me quite confused:
And I am not sure I understand it, and the numbers in it. It seems to me that
- $ \left[\mathbb{Q}\left(\rho\right):\mathbb{Q}\right] = 3 $, as $ m_{\rho}^{\mathbb{Q}}\left(x\right)=x^{3}-2 =f$, and its degree is $ 3 $.
- $ \left[\mathbb{Q}\left(\zeta\right):\mathbb{Q}\right] = 3 $ , as $ m_{\zeta}^{\mathbb{Q}}\left(x\right)=x^{3}-1 $, and its degree is $ 3 $.
Since both are simple algebraic extensions, and those are indeed their minimal polynomials, am I wrong? So I would expect both numbers on the bottom arrows to be 3 (?).
It was also noted that $ 6\mid\left[\mathbb{E}:\mathbb{Q}\right]=\deg m_{\rho}^{\mathbb{Q}\left(\zeta_{3}\right)}\cdot2\leq6 $ and I am not sure why this is true.
I saw this question but it didn't really help me.