Cube standing on a corner
This question has arisen from this post and the picture and the insights have been taken from the answers mentioned there.
$\quad\qquad\qquad\qquad\qquad\qquad\qquad$
In the above picture, a cube is standing on one of its corners. Let the cone lie on a $xz \text{ plane}$ and assume $y$-axis (the red line) passes through the centre of the cone and through one of the body diagonals of the cube. Now for the cube, imagine a plane passing though the points $QS$ and parallel to the $xz \text{ plane}$.
What I thought:
I thought, after looking at a dice for some time, that the $3$ vertices $QST$ would indeed form a triangle but the $3^{rd}$ vertex will be at a different height (not in the same plane), like the triangle $QST'$ below. So when a $xz \text{ plane}$ will cut the cube, what we'll get will be some polygon which with my level of understanding and imagination wasn't possible to fathom then.
 $\qquad$
$\qquad$ 
Image on the Left: Front View; $\qquad\qquad\qquad$Image on the Right: Top View
What it turned out to be:
It turned out that all the $3$ vertices, $QST$ indeed lie on single $xz \text{ plane}$, like $QST$ above, and thus form a triangle. Similarly it's true for the $3$ vertices above these (the vertices $U,V,W$). And add to that all the $4$ $xz \text{ planes}$ upon which all these vertices lie are at intervals of equal height!
I want to know that:
- How can we know whether a triangle forms and not some other polygon for the vertices $Q,S,T$ on the $xz \text{ plane}$ parallel to cone's base and passing through $1$ or more of the $3$ vertices (which may be an unfamiliar figure, maybe a pentagon or some quadrilateral, as below)?
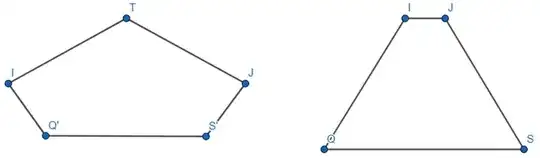
- Whether all the 3 vertices of the cube will lie on a plane parallel to $xz \text{ plane}$ and not on 2 planes parallel to $xz \text{ plane}$
- How to determine the height of these $xz \text{ planes}$ from one another?
- How will one calculate the centre and the radius for the obtained polygon in point 1?
[Note: Point 4 has a bit to do with the linked post (in case you don't get what I'm saying)]