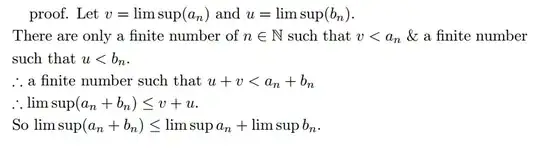1) "otherwise we clearly have the equality" -> why? It's not clear to me. :(
Rightly so, there need not be equality if $\limsup a_n = \limsup b_n = +\infty$. A possibility is that $\liminf a_n = -\infty$ and $b_n = -a_n$, in which case $a_n + b_n \equiv 0$ and hence $\limsup (a_n+b_n) < \limsup a_n + \limsup b_n$.
However, if $\limsup a_n = \limsup b_n = -\infty$, then both sequences "converge to negative infinity", and then so does their sum, so that equality holds.
And if $\limsup a_n = \limsup b_n = +\infty$, then we have the inequality
$$\limsup (a_n + b_n) \leqslant +\infty$$
which trivially holds. That also settles
2) "The inequality is trivially satisfied" -> why? even if the right side is +infinity, what if the left side is also +infinity?
We have a $\leqslant$, and everything is $\leqslant +\infty$.
3) $\{b_n\}$ is bounded -> I know there is a upper limit but I'm not sure if $b_n$ also has under limit.
It need indeed not be bounded from below. But all that is needed is that $b_n$ is bounded from above. Presumably, theorem 3.17 (b) only establishes an upper bound, and the author was a bit imprecise and meant only "bounded from above".
4) "one sees that $\limsup(a_n+b_n) = -\infty$" -> how is this so?
Because $a_n \to -\infty$ and $b_n \leqslant B$. $a_n \to -\infty$ means that for all $K$, there is an $n_0(K) \in \mathbb{N}$ such that for all $n \geqslant n_0(K)$, you have $a_n < K$. Choose $n_0(K-B)$ for $a_n + b_n$.
5) "Let $y \in \mathbb{R}$ be such that $a_{n_k} + b_{n_k} \to y$ for some sequence" -> How do we suppose such $y$ exists? what if there is no subsequence that converges?
Right, under the hypothesis, such a $y \in \mathbb{R}$ need not exist.
Consider
$$a_n = \begin{cases} 0 &, n \text{ even}\\ -n &, n \text{ odd}\end{cases};\quad b_n = \begin{cases}0 &, n \text{ odd}\\ -n &, n \text{ even}.\end{cases}$$
Then $a_n + b_n = -n \to -\infty$.
However, in that case, we have $\limsup (a_n+b_n) = -\infty \leqslant \limsup a_n + \limsup b_n$ since $-\infty \leqslant \text{ anything}$.
6) I'm not sure the equality between two different limits is made.
The $a_{n_{k_j}} + b_{n_{k_j}}$ is a subsequence of $a_{n_k} + b_{n_k}$, hence converges to the same limit. Since by assumption $a_{n_{k_j}} \to s$ and $b_{n_{k_j}} \to t$, we have $y = s+t$.