Conditional Expectation for Geometric Series - Dice problem

Question

A fair die is rolled repeatedly. Let $X$ be the number of rolls needed to obtain a 5 and $Y$ the number of rolls needed to obtain a 6. Calculate $E[X \mid Y=2]$.

I found a similar post of this same question here: A question on conditional expectation But I still do not understand the solution after reading it. If someone could hold my hand a little and provide a more thorough explanation I would really appreciate it.

This is what's going through my head:

Since $Y=2$, we roll a 6 on the second roll, meaning that we do not get a 6 on the first roll. Therefore, the first roll has a uniform distribution of the set $\{1,2,3,4,5\}$. We also know that $\Pr(X=2 \mid Y=2)=0$ because these events are mutually exclusive. We can apply the definition of expected value now and I let $Z=X \mid (Y=2)$.

$E[Z]=\sum\limits_{z=1,z \ge 3}^{\infty} z \cdot \Pr[Z] \tag{1}$

Now:

$\Pr[Z=1]=\Pr[X=1 \mid Y=2] = \Pr[5 \text{ on first roll} \mid 6 \text{ on second roll}]=1/5$

$\Pr[Z=2]=0$ as mentioned above.

Now I get confused when I calculate probabilities for $Z \ge 3$, and would appreciate some guidance:

$\Pr[Z=3]=\Pr[X=3 \mid Y=2] =\Pr[5 \text{ on third roll} \mid 6 \text{ on second roll}]$

So to calculate this probability, I thought I'd break this case down:

Question 1: I thought the first roll only can be from the set: $\{1,2,3,4\}$. Second roll = 6, and Third roll = 5. But I think the solution to this probability is: $(4/5)(1)(1/6)$. I don't see why the probability of the first roll is (4/5) because for this case, we can only get a 6 on the second roll. Can someone please explain and perhaps illustrate another example like $Pr[Z=4]$?

Question 2: My approach then was to find the equation for $\Pr[Z \ge 3]$ and then apply equation (1) to get the solution. Is this the best approach? I was reading another solution but did not understand it:

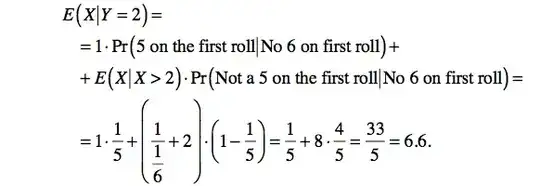
Thanks in advance.

Answer 1

This is a hard problem, but doable, even without partitioning the set or doing otherwise strange things you won't think of while taking Exam P. By definition we have $$E[X|Y=2]=\sum xPr(X|Y=2).$$ From here, you can use your reasoning skills to figure out what these probabilities. $$Pr(X=1|Y=2)=\frac 15,$$ because we have 5 equally likely possibilities. Since we're given $Y=2$, we DO NOT consider getting a 6 on the 1st try a possibility. $$Pr(X=2|Y=2)=0,$$ since you cannot have both a 5 and a 6 when you roll the die. $$Pr(X=3|Y=2)=\frac 45\cdot 1 \cdot \frac 16,$$ because you must not roll a 5 or 6 on the first roll, the second roll is given and happens with probability 1, and on the 3rd roll you roll a 5. This should be obvious, but these events are independent, so you multiply them. Finally consider $$Pr(X=4|Y=2)=\frac 45 \cdot 1 \cdot \frac 56 \cdot \frac 16 ,$$ because you must not roll a 5 or 6 on the first roll, the second roll has a value 6 with probability 1, you must not roll a 5 on the 3rd roll, and on the 4th roll you roll a 5. You can keep reasoning in this way but you should see the pattern. Now putting everything together, we have $$E(X|Y=2)= \sum xPr(X|Y=2)= 1(\frac 15) + 3(\frac 45)(\frac 16) + 4(\frac 45)(\frac 56)(\frac 16) + ...,$$ which is the same thing as the following series: $$\frac 15 + (\frac 45) \sum_{x=3}^{\infty}x(\frac 56)^{x-3}(\frac 16).$$ Now let $k=x-3$ (alternatively you can let $k=x-2$, but I prefer the former), we have $$\frac 15 + (\frac 45) \sum_{k=0}^{\infty}(k+3)(\frac 56)^k (\frac 16)= \frac 15 + (\frac 45) \sum_{k=0}^{\infty}k (\frac 56)^k (\frac 16) + (\frac 45)3 \sum_{k=0}^{\infty} (\frac 56) (\frac 16).$$ You should see a geometric random variable with $p=\frac 16$. To the right of the final equality, the first sum is the expected value and the second sum is summing the probability mass function over the sample space, which evaluates to 1. Lastly, in this form, $EK = \frac {1-p}p$. If you instead let k=$x-2$, then in that form $EK = \frac 1p$. Either way you'll arrive at the same answer. Continuing in the way we proceeded, our final answer is: $$ \frac 15 + \frac 45 \cdot \frac {1- \frac 16}{\frac 16} + \frac 45 \cdot 3 = 6.6 $$

Answer 2

Denote by $E_X$ the number of additional throws to get a first $5$ without additional conditions. Then $$E_X=1+{1\over 6}\cdot 0+{5\over 6}\cdot E_X\ .$$ This implies $E_X=6$. Now we know that $Y=2$, which means that the first throw was $\ne6$ and the second throw was $6$. It follows that the probability for a $5$ on the first throw, conditioned on this additional information, is ${1\over 5}$, and the probability for a $5$ on the second throw is $0$. Therefore we obtain $$E(X|Y=2)={1\over5}\cdot 1+{4\over5}\cdot(2+E_X)={33\over5}=6.6\ .$$