0

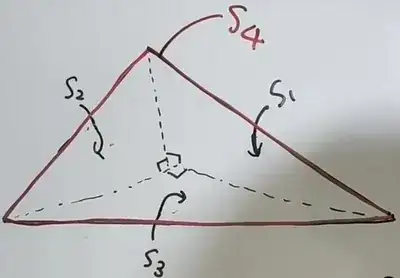
I should have depicted the following tetrahedron using tikz of tex. The image below is from this instagram post

enter image description here

$$ \color{fuchsia}{\underbrace{S_4^2= S_1^2+S_2^2+S_3^2}_{\text{I want to derive this} } } $$

$~ S_i ~$ represents the ith area of a triangle.

What I've done for deriving it are as follows.

$$\begin{cases} (0,0,0) \leftarrow~~\text{coordinates where the 3 right angle symbols gather}\\ (a,0,0) \leftarrow~~\text{coordinates on x-axis}\\ (0,b,0) \leftarrow~~\text{coordinates on y-axis}\\ (0,0,c) \leftarrow~~\text{coordinates on z-axis}\\ \end{cases}$$

Please assume that x-axis is along with left and y-axis is along with right and z-axis with vertical.

$$\begin{cases} S_1={1 \over 2 }bc\\ S_2={1 \over 2 }ac\\ S_3={1 \over 2 }ab\\ \end{cases}$$

So the remaining problem is to find out the formula of $~ S_4 ~$

What I've thought for it is to firstly find out the perpendicular line between $~ \text{AB} ~$ and $~ \text{C} ~$.

If that is done, then the coordinates on $~\text{AB} ~$ which is passed by that perpendicular line is known(we define this position as $~ \text{D} ~$ )

Hence

$$ S_4={1 \over 2 } \left( \text{AD} \cdot \text{CD} + \text{BD} \cdot \text{CD} \right) $$

But this way seems a bit complicated one I think.

Is there some more simpler way to derive the area of $~ S_4 ~$ ?

In the first place I don't know how to find the perpendicular line...

electrical apprentice
  • 1,519
  • A previous question has a link to a simple proof, that really relies on dropping perpendicular line from the origin to $AB$. – peterwhy Aug 02 '22 at 01:43
  • 1
    I am looking http://www.cut-the-knot.org/Generalization/pythagoras.shtml now which is on that post. – electrical apprentice Aug 02 '22 at 01:59
  • I think I derived the pink eqn. Since I am outside now, I will write an answer post later. – electrical apprentice Aug 02 '22 at 03:16
  • 1
    Sides of $S_4$ are $d=\sqrt{a^2+b^2}$, $e=\sqrt{a^2+c^2}$, $f=\sqrt{b^2+c^2}$. Let altitude to $f$ is $h$, then $\sqrt{d^2-h^2}=f-\sqrt{e^2-h^2}$, $d^2-h^2=f^2-2f\sqrt{e^2-h^2}+e^2-h^2$, $2f\sqrt{e^2-h^2}=f^2+e^2-d^2$, $2\sqrt{f^2e^2-f^2h^2}=b^2+c^2+a^2+c^2-a^2-b^2=2c^2$, $f^2e^2-f^2h^2=b^4$, $f^2h^2=f^2e^2-c^4$, $f^2h^2=(b^2+c^2)(a^2+c^2)-c^4=a^2b^2+a^2c^2+b^2c^2$. $S_4=fh/2$, then $S_4^2=S_1^2+S_2^2+S_3^2$. – Ivan Kaznacheyeu Aug 02 '22 at 11:46

1 Answers1

1

It is not necessary to derive an exact formula of a length of the perpendicular line. That is the key factor for proving the squared pink eqn.

$$\begin{align} p&:=\text{length of perpendicular line betwneen C and AB} \\ q&:=\text{length of line segment between the origin and AB} \\ d&:=\text{length of AB} \\ S_4^2&= \left({1 \over 2 }pd \right)^2\\&= {p^2 d^2 \over 4 }\iff 4S_4^2=p^2d^2\\ 4S_4^2&=p^2d^2\\ &=d^2 \left(c^2+q^2 \right)\\ &=c^2d^2+d^2q^2\\ &=c^2 \left(a^2+b^2 \right)+d^2q^2\\ &=\cdots\\ &=4S_1^2+4S_2^2+4S_3^2\\ \therefore S_4^2&=S_1^2+S_2^2+S_3^2 \end{align}$$

BTW using tikz to depict a figure is very time taking for me so far. But should I still use it? I wish I can use a tool which draw a figure with realtime response.

electrical apprentice
  • 1,519