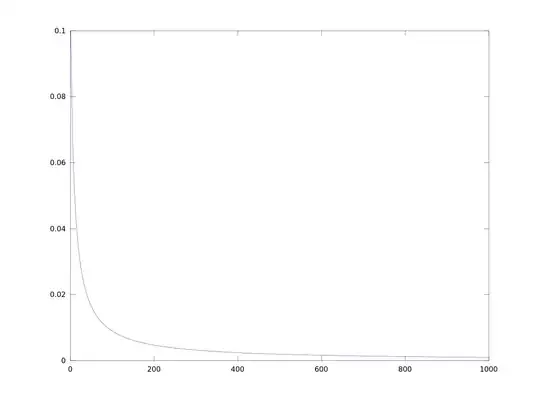
I am looking at the sequence $x_{n+1}=r\, x_n(1-x_n)$ where $r=1$.
Let's choose $x_1=1/2$ so as to make the sequence convergent to 0.
My question is: precisely how quickly does this sequence approach zero?
From my numerical experiments $\lim_{n\to\infty}n\,x_n=1$ seems likely. (That is $\mathrm O(1/n)$ convergence rate.) Do you have more precise result or some mathematical proof?
Let $y_n=\frac1{x_n}$. The recursion for these is $$y_{n+1}=y_n\cdot \frac1{1-x_n}=y_n\cdot (1+x_n+x_n^2+\ldots) = y_n+1+x_n+x_n^2+\ldots$$ As $x_n\to 0$ (assuming $0<x_0<2$) we see that $y_{n+1}-y_n\approx 1$, so there exists some $c$ such that $y_n\ge n+c$ and hence $x_n\le \frac1{n+c}$ for $n$ big enough.
Just wanted to add an illustration to show the logistic reccurence, plotted by octave. It has been made clear that the recurrence diverges for $x(0)>1$ or $x(0)<0$. I have chosen $x(0)$ to be $0.1$.
