Without a calculator, determine whether chords $AB, AC \text{ and }BD$ can divide a circle into five equal-area regions.

Question

Without a calculator, determine whether chords $AB, AC \text{ and }BD$ can divide a circle into five equal-area regions.

Context: I just made up this question.

I have only been able to answer the question with a calculator. Surely there must be some clever way to answer the question without a calculator.

Answer that uses a calculator:

Proof by contradiction: assume the answer is yes.
Let radius $=1$.
Call the centre $O$.
$\alpha=\angle{AOB}$
$\beta=\angle{AOC}$
$\text{Area}_{\text{minor segment }AB}=\dfrac12(\alpha-\sin{\alpha})=\dfrac{\pi}{5}\implies \alpha\approx2.1131$
$\text{Area}_{\text{segment }ADC}=\dfrac12(\beta-\sin{\beta})=\dfrac{2\pi}{5}\implies \beta\approx2.8248$
$\text{Area}_{\text{triangle}}=\dfrac{\pi}{5}\text{ and }AB=2\sin{\dfrac{\alpha}{2}}\implies ...\implies \angle{BAC}=\arctan{\left(\dfrac{\pi}{5\sin^2{\dfrac{\alpha}{2}}}\right)}\approx{0.692}$
But $\angle{BAC}=\dfrac12{\angle{BOC}}=\dfrac12{\left(2\pi-\alpha-\beta\right)}\approx{0.673}$, contradiction.
Therefore the answer is no.

UPDATE: I found essentially the same question, except it does not request a calculator-free solution. So it doesn't answer my question.

Answer 1

Second try (cleaner) Please refer to the diagram in my other answer.

By naming $2\theta=\widehat{BOA},\, 2\varphi=\widehat{AOC}$ and by imposing that the circle segments on $AB,AC,BD$ have the correct areas we end up with $$ \theta-\frac{1}{2}\sin(2\theta)=\frac{\pi}{5},\qquad \varphi-\frac{1}{2}\sin(2\varphi)=\frac{2\pi}{5}.\tag{A}$$ In the triangle $ABE$ we have $AB=2\sin\theta$ and $\widehat{ABE}=\pi-(\theta+\varphi)$, so $$ [ABE] = -\sin^2(\theta)\tan(\theta+\varphi) \tag{B}$$ and given $(A)$ it is enough to show that $(B)$ cannot be equal to $\frac{\pi}{5}$.
$f(x)=x-\frac{\sin(2x)}{2}$ is non-negative, convex and increasing from $0$ to $\pi/2$ on $[0,\pi/2]$, with $f'(x)=2\sin^2(x)$. We have $\theta\approx \pi/3$ and by a single step of Newton's method with starting point $\pi/2$ we have $\varphi\approx 9\pi/20$. Precisely $\theta > \pi/3$ and $\varphi < 9\pi/20$, and the error of these approximations is controlled by the fact that $1\leq f'\leq 2$ in $[\pi/4,\pi/2]$. In particular

$$ \theta < \frac{\pi}{3}+\left(\frac{\pi}{5}-f(\pi/3)\right) $$ $$ \varphi > \frac{9\pi}{20}-\left(f(9\pi/20)-\frac{2\pi}{5}\right)\tag{C}$$ such that $[ABE]$ is very close to $\frac{3}{4}\tan\left(\frac{13}{60}\pi\right)$.
The impossibility of the pentasection then follows from the proof of the following inequality: $$ \tan\left(\frac{13\pi}{60}\right)<\frac{4\pi}{15}=\frac{16\pi}{60}\tag{D} $$which is equivalent to $$ \frac{1-\tan(\pi/30)}{1+\tan(\pi/30)} < \frac{4\pi}{15}\tag{E} $$ or to $$ \tan\left(\frac{\pi}{30}\right) > \frac{15-4\pi}{15+4\pi} \tag{F}$$ which just follows from $$ \tan\left(\frac{\pi}{30}\right) > {\color{red}{\frac{\pi}{30}}} > \frac{15-4\pi}{15+4\pi} \tag{G}$$ since $\pi > \frac{15}{8}(\sqrt{113}-9).$

Answer 2

Let us assume that the radius of the circle is $1$ and let $\widehat{BOA}=2\theta$.
Then $\theta$ is the unique solution of $\theta-\frac{1}{2}\sin(2\theta)=\frac{\pi}{5}$ and $AB=\sin(2\theta)$.
$[AEB]=\frac{\pi}{5}$ then implies $ME=\frac{\pi}{5\sin\theta}$ and $AE=EB=\sqrt{\sin^2\theta+\frac{\pi^2}{25\sin^2\theta}}$.
The height of the circle segment with base $AB$ is $1-\cos\theta$, so by naming $P$ the antipode of $N$ we have $EP=1-\cos\theta+\frac{\pi}{5\sin\theta}$ and $EN=1+\cos\theta-\frac{\pi}{5\sin\theta}$. By the chords theorem $EN\cdot EP = EC\cdot EA$, hence

$$ EC = \frac{1-\left(\cos\theta-\frac{\pi}{5\sin\theta}\right)^2}{\sqrt{\sin^2\theta+\frac{\pi^2}{25\sin^2\theta}}}$$ and by the similarity between $EAB$ and $ECD$ we have

$$ CD = \frac{1-\left(\cos\theta-\frac{\pi}{5\sin\theta}\right)^2}{\sin^2\theta+\frac{\pi^2}{25\sin^2\theta}}\cdot 2\sin\theta$$ and

$$ \widehat{DOC} = 2\arcsin\left(\frac{1-\left(\cos\theta-\frac{\pi}{5\sin\theta}\right)^2}{\sin^2\theta+\frac{\pi^2}{25\sin^2\theta}}\cdot \sin\theta\right).$$ The length of $OE$ is $\frac{\pi}{5\sin\theta}-\cos\theta$, hence the area of the quadrilateral $DOCE$ equals

$$ [DOCE] = \left(\frac{\pi}{5\sin\theta}-\cos\theta\right)\left(\frac{1-\left(\cos\theta-\frac{\pi}{5\sin\theta}\right)^2}{\sin^2\theta+\frac{\pi^2}{25\sin^2\theta}}\cdot \sin\theta\right) $$ and the area of the portion of the circle bounded by $E,D,C$ equals

$$\arcsin\left(\frac{1-\left(\cos\theta-\frac{\pi}{5\sin\theta}\right)^2}{\sin^2\theta+\frac{\pi^2}{25\sin^2\theta}}\cdot \sin\theta\right)-\left(\frac{\pi}{5\sin\theta}-\cos\theta\right)\left(\frac{1-\left(\cos\theta-\frac{\pi}{5\sin\theta}\right)^2}{\sin^2\theta+\frac{\pi^2}{25\sin^2\theta}}\cdot \sin\theta\right).$$

Few steps of Newton's method give $\theta\approx 1.05657$, hence the last expression is $\approx 0.552681$ while $\pi/5\approx 0.628319$, proving that the wanted pentasection is impossible.

Answer 3

$\huge{\text{Preliminaries}}$

This answer does not require a calculator, but assumes that we can add/subtract/multiply/divide numbers of up to five digits, and uses the following facts:
$3.1415<\pi<3.1416$
$1.414<\sqrt2<1.415$
$1.732<\sqrt3<1.733$
$\sqrt{5-2\sqrt5}<0.727$ which can be proved:

$\sqrt5>2.236$
$5-2\sqrt5<0.528$
$\sqrt{5-2\sqrt5}<\sqrt{0.528}<\sqrt{0.727^2}=0.727$

$\tan{\dfrac{\pi}{5}}=\sqrt{5-2\sqrt5}$ which is proved here.

$\huge{\text{Proof by contradiction: assume the answer is yes}.}$

$\huge{\text{Define $\alpha$ and $\beta$}.}$

Let radius $=1$.
Call the centre $O$.
$\alpha=\angle{AOB}$
$\beta=\angle{AOC}$

$\huge{\text{Show that }\alpha>2.1.}$

$2\times\text{Area}_{\text{minor segment }AB}=\alpha-\sin{\alpha}=\dfrac{2\pi}{5}$

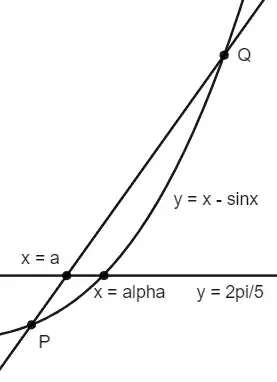
Between $P\left(\dfrac{2\pi}{3},\dfrac{2\pi}{3}-\dfrac{\sqrt3}{2}\right)$ and $Q\left(\dfrac{3\pi}{4},\dfrac{3\pi}{4}-\dfrac{\sqrt2}{2}\right)$, the curve $y=x-\sin{x}$ is concave up, so the curve lies to the right of line segment $PQ$.
We can show that $P$ is below $y=\dfrac{2\pi}{5}$, and $Q$ is above $y=\dfrac{2\pi}{5}$:

$\dfrac{2\pi}{3}-\dfrac{\sqrt3}{2}<\dfrac{2(3.15)}{3}-\dfrac{1.7}{2}=1.25<1.256=\dfrac{2(3.14)}{5}<\dfrac{2\pi}{5}$
$\dfrac{2\pi}{5}<\dfrac{2(3.2)}{5}=1.28<1.45=\dfrac{3(3)}{4}-0.8<\dfrac{3\pi}{4}-\dfrac{\sqrt2}{2}$

Let $a=$ x-coordinate of intersection of $y=\dfrac{2\pi}{5}$ and line segment $PQ$.

$\alpha >a=\dfrac{\frac{2\pi}{5}+\frac{9\sqrt3}{2}-4\sqrt2}{1+\frac{6}{\pi}(\sqrt3-\sqrt2)}>\dfrac{0.4(3.14)+4.5(1.732)-4(1.415)}{1+\frac{6}{3.14}(1.733-1.414)}=\dfrac{3.39}{\frac{5.054}{3.14}}>\dfrac{3.39}{1.61}>2.1$

$\huge{\text{Show that }\beta>2.82.}$

$2\times\text{Area}_{\text{segment }ADC}=\beta-\sin{\beta}=\dfrac{4\pi}{5}$

Between $R\left(\dfrac{5\pi}{6},\dfrac{5\pi}{6}-\dfrac{1}{2}\right)$ and $S\left(\pi,\pi\right)$, the curve the curve $y=x-\sin{x}$ is concave up, so the curve lies to the right of line segment $RS$.
We can show that $R$ is below $y=\dfrac{4\pi}{5}$, and $S$ is above $y=\dfrac{4\pi}{5}$:

$\dfrac{5\pi}{6}-\dfrac{1}{2}<\dfrac{5(3.6)}{6}-\dfrac{1}{2}=\dfrac{4(3)}{5}<\dfrac{4\pi}{5}$
$\dfrac{4\pi}{5}<\pi$

Let $b=$ x-coordinate of intersection of $y=\dfrac{4\pi}{5}$ and line segment $RS$.

$\beta >b=\dfrac{\frac{4\pi}{5}+3}{1+\frac{3}{\pi}}>\dfrac{0.8(3.1415)+3}{1+\frac{3}{3.1415}}>\dfrac{5.5132}{1.955}>2.82$

$\huge{\text{Show that }\angle{BAC}<0.6816}.$

$\angle{BAC}=\dfrac{1}{2}{\angle{BOC}}=\dfrac{1}{2}{\left(2\pi-\alpha-\beta\right)}<\dfrac{1}{2}(2(3.1416)-2.1-2.82)=0.6816$

$\huge{\text{Show that }\alpha<2.12.}$

$2\times\text{Area}_{\text{minor segment }AB}=\alpha-\sin{\alpha}=\dfrac{2\pi}{5}$

Between $(0,0)$ and $(\pi,\pi)$, the curve $y=x-\sin{x}$ is concave up, so the curve lies to the left of the tangent to the curve at $x=\dfrac{2\pi}{3}$.
Let $c=$ x-coordinate of intersection of $y=\dfrac{2\pi}{5}$ and the tangent to the curve at $x=\dfrac{2\pi}{3}$.

$\alpha<c=\dfrac{\sqrt3}{3}+\dfrac{22\pi}{45}<\dfrac{1.74}{3}+\dfrac{22(3.15)}{45}=2.12$

$\huge{\text{Show that }5-5\cos{\alpha}<7.62.}$

For $\dfrac{\pi}{2}<x<\pi$, the curve $y=5-5\cos{x}$ is concave down, so the curve lies below the tangent to the curve at $x=\dfrac{2\pi}{3}$, which has equation $y=\dfrac{5\sqrt3}{2}\left(x-\dfrac{2\pi}{3}\right)+7.5$.

$5-5\cos{\alpha}<5-5\cos{2.12}<\dfrac{5\sqrt3}{2}\left(2.12-\dfrac{2\pi}{3}\right)+7.5<5.3(1.733)-\dfrac{5(3.141)(1.732)}{3}+7.5<7.62$

$\huge{\text{Show that }\angle{BAC}>0.6817}.$

In the diagram of the circle and chords, $\text{Area}_{\text{triangle}}=\dfrac{\pi}{5}\text{ and }AB=2\sin{\dfrac{\alpha}{2}}\implies\angle{BAC}=\arctan{\left(\dfrac{2\pi}{5-5\cos{\alpha}}\right)}$
$\angle{BAC}=\arctan{\left(\dfrac{2\pi}{5-5\cos{\alpha}}\right)} > \arctan{\left(\dfrac{2\pi}{7.62}\right)}>\arctan{\left(\dfrac{2(3.14)}{7.62}\right)}>\arctan{0.82}$

Between $T\left(\sqrt{5-2\sqrt5}, \dfrac{\pi}{5}\right)$ and $U\left(1, \dfrac{\pi}{4}\right)$, the curve $y=\arctan{x}$ is concave down, so the curve lies above line segment $TU$, which has equation $y=\dfrac{\frac{\pi}{20}}{\sqrt{5-2\sqrt5}-1}(1-x)+\dfrac{\pi}{4}$.

$\angle{BAC}>\arctan{0.82}>\dfrac{\frac{\pi}{20}}{\sqrt{5-2\sqrt5}-1}(1-0.82)+\dfrac{\pi}{4}>\dfrac{\frac{3.141}{20}}{0.727-1}(0.18)+\dfrac{3.141}{4}>0.6817$

$\huge{\text{Contradiction}}.$

$\huge{\text{Therefore the answer is no}}.$