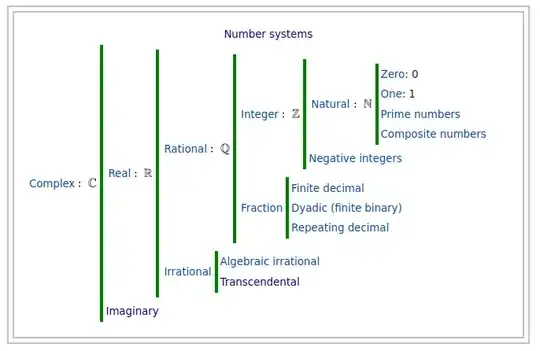
On Wikipedia > Number > Classification there is this diagram:
A. This diagram implies that the irrational numbers are a subset of solely the real numbers. But afaik, that's not true, because any number, which is not rational, is an irrational number, and thus all imaginary numbers are irrational, because they are not rational.
I think the diagram suffers from the fact that some irrational numbers are real numbers and some are complex numbers with non-zero imaginary part. So irrational numbers are neither a subset of solely the real numbers nor solely of $\mathbb{C}\setminus\mathbb{R}$.
B. Moreover, the diagram seems to imply that the complex numbers consist solely of real numbers and purely imaginary numbers. Afaik, all complex numbers which have both, a non-zero real part and a non-zero imaginary part, are neither real nor imaginary, so they are missing in the diagram.
Is this diagram misleading? Or is it even wrong?