3

in the book that I'm studying, The Rule of Existential Generalization (EG) is stated as:

If a formula S results from a formula R by substituting a variable v for every occurrence in R of some ambiguous (or proper) name, then ($\exists v$)S is derivable from R.

But from this we cannot conclude that $\exists x(x = 1)$ is derivable from $1=1$

Instead, if we substitute '$x$' for every occurrence of '$1$' in R, what we get is that $\exists x(x = x)$ is derivable from $1=1$

ADDENDUM

Which book says that?

The above is excerpted from p. 83 of Patrick Suppes' Introduction to Logic.

ryang
  • 38,879
  • 14
  • 81
  • 179
JCAL
  • 234
  • 1
  • 12
  • 1
    I think this is just because this isn't the only case for existential generalization: in other words, I think you can derive $\exists x (x = 1)$ from $1 = 1,$ just not with this exact rule. – Stephen Donovan Jul 21 '22 at 04:06
  • Perhaps the argument could go as follows: we substitute the variable x for every occurrence of a proper name in ‘1 = 1’ since there are no occurrences of proper names in ‘1=1’ the result is then just what we started with. But strictly speaking ‘1’ is a proper name.. I dunno – JCAL Jul 21 '22 at 04:11
  • 3
    Which book says that? – Peter Smith Jul 21 '22 at 05:57
  • Patrick Suppes "Introduction to Logic" – JCAL Jul 21 '22 at 05:59
  • 1
    As per answers below, the rule is stated correctly; see Existential Introduction in ND: the rule is "from $\varphi[x/a]$ derive $\exists x \varphi$. In your case we have that $\varphi$ is $x=1$ and $\varphi[x/a]$ is $1=1$ where $1$ is the term $a$. – Mauro ALLEGRANZA Jul 21 '22 at 06:03

2 Answers2

4

in the book that I'm studying, The Rule of Existential Generalization:

If a formula S results from a formula R by substituting a variable v for every occurrence in R of some ambiguous (or proper) name, then ($\exists$v)S is derivable from R.

But from this we cannot conclude that $\exists x( x = 1)$ is derivable from $1=1$

You're right, because that above rule has been stated wrongly.

Let's pare down its phrasing:

  • If replacing every occurrence of <some ambiguous or proper name> in formula R with <variable $v$> changes R to S, then $(\exists v\;$S) is derivable from R. $\tag✗$

Here's one way to correct it (note also that the additional adjective “free” is crucial):

  • If replacing every free occurrence of variable $v$ in formula S with term $\tau$ changes S to R, then $(\exists v\;$S) is derivable from R. $\tag✓$

The above rule is also called Existential Introduction (for completeness, I should also point out, that the above derivation does not discharge any assumption). Two of its counterparts: Existential Elimination and Universal Introduction.

Lastly, the above inferential rule in action: enter image description here

ryang
  • 38,879
  • 14
  • 81
  • 179
  • 1
    Thus in the correct version to derive $\exists x(x = 1)$ from 1 = 1 we need to replace the free variable 'x' in "x = 1" with term '1' and in doing so we see that x = 1 changes to 1 = 1 hence the result. Is this correct? – JCAL Jul 21 '22 at 06:03
  • Open Logic Project does not use Suppes' system. OLP uses introduction rule: "Thus, inferring ∃x P (t, x) from P (t, t) is a correct application of ∃Intro—you may “replace” one or more, and not necessarily all, occurrences of t in the premise by the bound variable x" – Tankut Beygu Jul 21 '22 at 18:18
  • 1
    Is the book's rule really wrong though? Especially if the book requires unique bound variable names or prior specified conditions on substitution (I don't have the book, just speculating). It seems at worst potentially incomplete, although I have a hard time thinking of what could be added to the book's rule that could result in the more general rule, short of just stating the general rule. – DanielV Jul 22 '22 at 03:04
-4

As the question has unexpectedly taken an instructive turn, I need to revise my answer from beginning to end. I shall explain why Patrick Suppes' statement of the rule is not wrong, though his system might seem peculiar (well, he was an eminent philosopher at the end of the day), and why $\exists x(x=1)$ cannot be derived from $1 = 1$ at one step from EG-rule in his system.

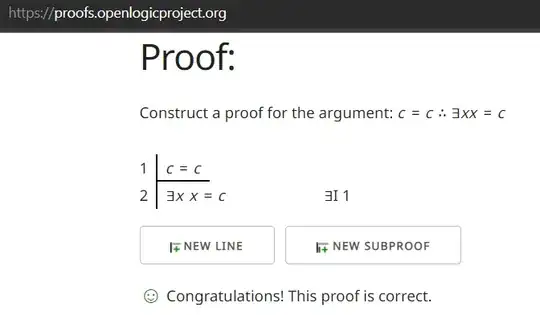
This is the definition of the definition of existential introduction rule from the text of Open Logic Project (p. 276):

enter image description here

So, Suppes' definition is wrong and Open Logic Project's is right? No, neither one is wrong; if one gives the same input, one gets the same output from both of them, the difference resides in between. They are just different systems of proof that serve the same ends, each with its vices and virtues. A necessity is that one ought to absolutely keep in the system one has begun with all the way through, even if an obvious line appears counter-intuitively hard to derive.

In contrast to many contemporary books on mathematical logic, Suppes extensively offers verbal accounts merged with semantic considerations in a system with specific features. To see the relevant divergence in Suppes' system, it may be helpful first to examine a proof in a system that today's readership is more familiar. The proof is a modification of the one Allegranza has given as an answer using the system in H. Enderton's A Mathematical Introduction to Logic, since we have $1 = 1$ as a premiss at present ($y$ is substituted by $1$, see the referred answer for the annotations):

  1. $1 = 1$
  2. $\forall x\neg(x = 1)\rightarrow\neg(1 = 1)$
  3. $(1 = 1)\rightarrow\neg(\forall x\neg(x = 1))$
  4. $\neg(\forall x\neg(x = 1))$
  5. $\exists x(x = 1)$

Focus on the subformula $x = 1$. If $1$ is an individual constant of the language, this open formula can be readily constructed by the syntactic formation rules. Anyhow, it has to occur in some line. Because we need the statement '$x$ is $1$'; by themselves, '$x$ is $x$' or '$1$ is $1$' does not suffice in this system in order to derive $\exists x(x = 1)$. We'll see a similar requirement in Suppes' system.

The following are the relevant directions Suppes gives in the book:

R1

(p. 85)

R2

(p. 104)

R3

(p. 104)

It should be remarked that Suppes defines open formulas as "formulas which have no quantifiers" (unlike the standard definition). Accordingly, we have not only the system-given open formula $y = y$, but also $1 = 1$ as the premiss. But how shall we proceed further? Given the EG-rule that dictates us a uniform replacement, the last rule seems of no use to deduce from $y = y$ and $1 = 1$ to $y = 1$ to conclude $\exists x(x = 1)$.

In Suppes' system, terms are divided into three classes: proper names, ambiguous names ("temporary constants", more on them below) and variables. The details of this system cannot be summarised here, but the key idea to proceed further is, assuming that $1$ is in the domain of discourse, again an introduction of a formula that says "... is $1$" (by a proper name $a = 1$ or an ambiguous name $\alpha = 1$).

We have seen that some systems demand an explicit designation like $x = 1$, some others do not and find it sufficient that a name exists in the language. Each proof system has a "design philosophy" behind it and authors have their individual concerns. However, even a cursory discussion of these is too far-fetching.

Let us consider the issue the OP rightly draws our attention to. On p. 78, Suppes says

enter image description here

Isn't it incoherent to derive the existential formula "immediately" given the EG-rule? This cannot be said to be incoherence, but an unfortunate result of Suppes' style dispersing the features of his system here and there in the book.

As mentioned above, Suppes describes a class of terms he calls ambiguous names to facilitate quantifier rules. He remarks in the preface that

enter image description here

An epsilon term $\epsilon xA(x)$ picks out some $x$ whose only characteristic is to satisfy $A(x)$. Employing this device with an ambiguous name $\alpha$, we replace $\frac{1}{2}$ in the formula

$\frac{1}{2}=\frac{1}{2}$, then

$\frac{1}{2}=\alpha$

since $\alpha$ is a name whose only defining property is to denote $\frac{1}{2}$. Thus,

$\exists x(\frac{1}{2}=x)$

follows. This is what Suppes calls "immediate", as I understand him.

Addendum

It may be useful to explicate the notion of ambiguous name a bit more. It is, in fact, a representation of a familiar device.

Consider a common phrase from mathematical discourse: "Let $\alpha$ be an even number, . . ." What is $\alpha$ here?

Suppes would respond like this: It is not genuinely a variable, it does not vary across a range of values as the argument of a function does. It is not a number name, either; it is not one of the names two, four, six, . . . It does not designate something properly, its status is ambiguous. Actually, it is a temporary number name we introduce to carry out our discussion and has no identity in itself beyond this.

Tankut Beygu
  • 2,331
  • 3
    This answer is misleading. There are logics (free logics) in which terms may fail to denote - these have been developed to try to address the issues you raise in your answer. But these logics are nonstandard. In standard first-order logic, $\exists x, x=t$ is derivable for any term $t$. – Alex Kruckman Jul 21 '22 at 12:28
  • 1
    @AlexKruckman Take notice that I do not say $\exists x(x = t)$ is not derivable. I say: 1. The rule is correctly stated, 2. From $1 = 1$ one cannot derive $\exists x(x = 1)$ by existential generalisation. So: what the OP tries to do is wrongheaded, what the OP sees obliged to do is the proper derivation according to the rule of EG. – Tankut Beygu Jul 21 '22 at 13:27
  • Notice on page 78 (Before EG is introduced) the author derives $\exists x(x = \frac{1}{2}$ from $\frac{1}{2}= \frac{1}{2}$ so the author is being inconsistent then also, which actually led me to the question. From your above comment and post Suppes also makes the same mistake using his formation of EG – JCAL Jul 21 '22 at 21:31
  • 1
    @JCAL I'll look into it -tomorrow. For the moment, I should remark that Copi et al's proof system in their Introduction to Logic employs the same rule as Suppes', that is, this form of the rule is not unusual. One should work in a proof system consistently, not in the fashion, one rule from Fitch, the other from Kelly and from others at will. That makes one only less knowledgeable about logic. – Tankut Beygu Jul 21 '22 at 21:43
  • 1
    Thanks for the comment!! I am solely trying to work in Suppes system, as that is the book I’m currently reading! Let me know what you discover when you look into it! – JCAL Jul 21 '22 at 21:46
  • @AlexKruckman I have entirely revised my answer. If you see anything problematic, do tell me; I benefit from this discussion. – Tankut Beygu Jul 22 '22 at 23:06
  • @JCAL I hope I have clarified your concern. But, of course, my answer cannot be a substitute for a thorough explanation of Suppes' system. – Tankut Beygu Jul 22 '22 at 23:09
  • I personally like Suppes Introduction to logic, while it is elementary and there are certainly more rigorous books, one must start somewhere! – JCAL Jul 23 '22 at 04:20
  • My concern however is that $\frac{1}{2}$ is not actually an ambiguous name. Notice on page 84 (last paragraph) Suppes remarks that we cannot interpret ambiguous names in the same way we interpret proper names. He remarks that from $(\exists x) Fx$ We derive $Fa$ but ‘$a$’ cannot be regarded as a proper name according to ES. – JCAL Jul 23 '22 at 04:41
  • Right, $\frac{1}{2}$ is not an ambiguous name; for the sake of argument, we replace it with an ambiguous name. The warning you have mentioned is given in the context of existential specification (instantiation). We could replace it with a proper name as well, but proper and ambiguous names can be deemed similar to global and local variables in computer programming, it is a good practice to keep the permanent and the temporary separate. When things get larger and deeper, complications may occur, otherwise. – Tankut Beygu Jul 23 '22 at 16:49
  • @JCAL I began logic with Kalish and Montague's Logic: Techniques of Formal Reasoning and still keep a copy of it. You may wish to take a look at it (freely readable, there is not much change from the first edition to the second). – Tankut Beygu Jul 23 '22 at 16:55
  • But in Suppes ES we cannot derive $1=1$ from $\exists x(x=1)$ since if we follow the rule precisely $1$ is not a ambiguous name. In your above comment though you say we may substitute proper names when applying ES? – JCAL Jul 23 '22 at 17:56
  • I think your analysis of what's going on in Suppes is a valuable contribution. But the answer is awfully long - all the text before "Now, we can talk about...", as well as the section on semantic considerations, could be cut without losing anything. Also, as long as you're quoting extensively from the text, it would be nice to see a quote justifying the step $\frac{1}{2} = \alpha$ from $\frac{1}{2} = \frac{1}{2}$. Indeed, I think the treatment of "ambiguous names" is at the core of the confusion here. – Alex Kruckman Jul 23 '22 at 18:40
  • @AlexKruckman thanks. I made hasten to avert misunderstanding. – Tankut Beygu Jul 23 '22 at 19:09
  • @JCAL Let us proceed with the wording of the ES-rule definition: We replace the free variable $x$ in $R$ (i.e., in $x=1$), and obtain $\alpha=1$. $\alpha$ is a term and the identity rules are applicable to it. We have $\alpha =\alpha$, disambiguating $\alpha$, we get $1=1$. That is, when a proper name is assigned to an ambiguous name, it is disambiguated. An ambiguous name must not occur in the last line of a derivation. Notice that to write the line $t_{1}=t_{2}$, it is not necessary that both terms are of the same class, one may be a proper name and the other may be a variable, etc. – Tankut Beygu Jul 23 '22 at 19:13
  • Ahh okay thank you.. I have not gotten to the part on “Logic of identity” hence my confusion. Also quick question, do you like Patrick Suppes book on logic? – JCAL Jul 23 '22 at 20:12
  • Also if your line of reasoning is correct what’s then stopping us from deriving $2=2$ from $\exists x(x = 1)$ since that procedure would then be exactly the same wouldn’t it? – JCAL Jul 23 '22 at 20:26
  • I don't think so. See the table of basic rules of inference on p. 99. The system imposes elaborate restrictions based on flags and subscripts on derivation. – Tankut Beygu Jul 23 '22 at 20:41
  • @AlexKruckman I have shortened the answer and appended an addendum about the notion of ambiguous names. – Tankut Beygu Jul 24 '22 at 18:58