You're very fortunate! The exponentiation of complex numbers involves some very beautiful geometry! We could do this through some algebraic manipulation easily enough, but it is more interesting for us to try and see what's going on!
Let's start with raising a complex number to a real power.
In you question, you tried to do this by distributing exponentiation over addition: $(a+bi)^z \to a^z + bi^z$... While this would make things more convenient for us, exponentiation, unfortunately, does not work like this. For example: $(1+1)^2 = 4$ but $1^2 + 1^2 = 2$.
Recall that, for multiplication, it is often easier to think of complex numbers in terms of argument (angle from the real axis) and magnitude (distance from zero). In the following lovely picture from Wikipedia, $\phi$ is the angle and $r$ is the magnitude.
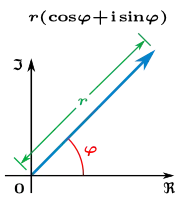
That is, instead of writing $z$ as $a+bi$, we can write it as $r(\cos(\theta) + i\sin(\theta))$. Since $\cos(\theta) + i\sin(\theta)$ moves along the complex unit circle, we can get all values. I won't prove it here, since it would be somewhat non-trivial and you used it in your question, but $e^{i\theta} = \cos(\theta) + i\sin(\theta)$. So we can write $$z = r*e^{i\theta}$$
The reason this is so nice for multiplication is that when we multiply, the magnitudes add and the arguments add. For example:
$$r_1e^{i\theta_1}*r_2e^{i\theta_2} = r_1*r_2e^{i(\theta_1+\theta_2)}$$
(This follows algebraically, in addition to being a restatement of what I said earlier. So, if you accept Euler's formula, this verified my claims about arguments adding in multiplication.)
When we exponetiate to a natural number, we're multiplying something by itself, multiple times, so the magnitude is exponentiated and the argument scales.
$$(re^{i\theta})^n = r^n * e^{in\theta}$$
(You can verify this algebraicly, and note that for that, $n$ could be anything you want!)
In his book, Visual Complex Analysis, Needham gives a very beautiful visualization of the geometry of this:
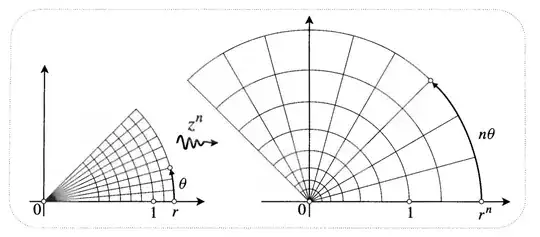(Note that this is an excerpt from his book used under fair use.)
(Actually, Needham gives lots of awesome visualizations like this, and I'd encourage people to look at the book. It's an amazing work of mathematical exposition.)
Notice how argument scales as we raise the power, and magnitude is exponentiated!
Another way to look at this is using colors! We map each complex number to a color, with hue being argument and brightness being magnitude. In this example, we square:
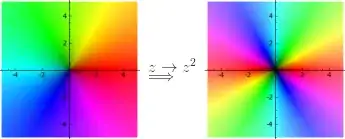
Notice how the argument (hue) cycles twice as fast in the image as we go around, because it changes twice as fast (being multiplied by 2)!
Raising to a complex power!
Let's start by just looking at a visualization of what happens when we raise to powers on the complex unit circle. The proper version is animated, and you can see it here, but since i can't embed a GIF, here's a still image:
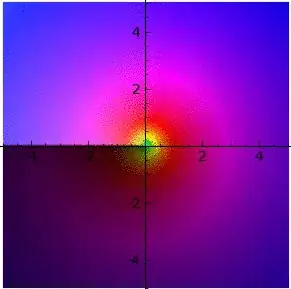
The argument and magnitude switch places! Something really interesting must happen!
A little algebraic manipulation can give us a lot of insight. First, note that we can represent $re^{i\theta}$ as $e^{\ln(r) + i\theta}$ instead. Then:
$$(e^{\ln(r) + i\theta})^{a+bi} = e^{(\ln(r) + i\theta)(a+bi)}$$
If we just raise to the power of $i$, we get:
$$(e^{\ln(r) + i\theta})^{i} = e^{i\ln(r) -\theta} = e^{-\theta}*e^{i\ln(r)}$$
Switching the argument and radius (modulus), as we saw in the animation!
But what's the answer?
Well, if we really want to, we can completely algebraicly expand things:
$$(e^{\ln(r) + i\theta})^{a+bi} = e^{(\ln(r) + i\theta)(a+bi)}$$
$$e^{(\ln(r) + i\theta)(a+bi)} = e^{\ln(r)a + ib\ln(r) + ia\theta - b\theta}$$
$$e^{\ln(r)a + ib\ln(r) + ia\theta - b\theta} = e^{\ln(r)a- b\theta} * e^{i(b\ln(r) + a\theta) }$$
But I think we learn a lot more from the previous work.
