I have problem regarding random number generation. Suppose I have disc of radius $r$. $$ \begin{align} x&=r\cos(\theta)\\ y&=r\sin(\theta)\\ z&=0 \end{align} $$ I rotate the co-ordinate. So new co-ordinate is $$ \begin{align} X&=x\cos(\phi)+z\sin(\phi)\\ Y&=y\\ Z&=-x\sin(\phi)+ z\cos(\phi) \end{align} $$ I want to generate $r$, $\theta$ and $\phi$ by random number such that I get equal probability in all space. I used $$ \begin{align} r&=r_{\text{max}}\sqrt{\mathrm{random}(N)}\\ \theta&=2\pi\,\mathrm{random}(N)\\ \phi&=\phi_{\text{min}}+\mathrm{random}(N)*(\phi_{\text{max}}-\phi_{\text{min}}) \end{align} $$ But it does not work I think. Can anybody help me?
-
You should clarify this “equal probability in all space”. It might be best to specify which parts of your parameter space should have equal probability. Do you want the probability of a volume of space to be proportional to the volume itself, as long as the volume lies within the sphere of radius $r$? – MvG Jul 22 '13 at 14:18
-
So the main thing is I want to put that N random number in a box of size(DXDY). Suppose they have flat distribution F=box or gaussian function of r. So, it's like m=(X-xmin)nx/DX and n=(Y-ymin)*ny/DY. H(m, n)=H(m, n)+F. By plotting H, I want to see the distribution the N number of points regularly distributed. – user87267 Jul 22 '13 at 14:59
-
I am still unsure of what you want. Do yo want a uniformly distributed random point in a sphere of radius $r$? – robjohn Jul 22 '13 at 15:15
-
Yes but in my case the sphere is not full. ϕmin<ϕ<ϕmax instead of 0 to pi. – user87267 Jul 22 '13 at 15:32
-
Okay, so the shape is like an orange with two opposing wedges cut out. – robjohn Jul 22 '13 at 15:48
-
In your first comment, you talk about a box DX*DY, but the question is about 3D. Which is it? In your second comment you talk about restricting the range of $\phi$, but that usually ranges from $0$ to $2\pi$. Are you really restricting the range of $\theta$?. I will assume that. – Ross Millikan Jul 22 '13 at 16:25
-
Here is a confusion.I took as θ (azimuthal angle) 0 to 2pi. ϕ(polar angle): ϕmin<ϕ<ϕmax. So it's kind of bicone in XZ plane because my rotation is around y axis. Now consider any func: F(r)=exp(-r^2); It will show some spike as it's random. I want to obtain this function in a 2D box mainly in XY plane so that I can see a nice gaussian in 2D but as a function (X,Y). Like I put all N number of random points in BOX to obtain a new function F(X, Y). So, I say my box goes from xmin to xmax(say) and same for y. It will have 100 *100 pixels (like I put N points in 2D hist) & I want uniform density. – user87267 Jul 22 '13 at 16:55
-
If your rotation is around the $y$-axis, in the $x{-}z$ plane, you should see circles, not cones. What is BOX? Doing my best to understand what you are trying to ask, I have tried to generate the region you are looking for in this image. Is that correct? – robjohn Jul 22 '13 at 17:47
-
Either the question or the comment needs to be corrected. In the question, you describe a region that looks like this image rather than like this image, which is what you describe in you latest comment. – robjohn Jul 22 '13 at 19:14
-
As i told that I have to use the equation I have written. It just a disc having random inclination between ϕmin to ϕmax with respect to distance observer. Using my equation I got a picture as u have shown (http://i.stack.imgur.com/tOpPN.png). The only question is how to take r, θ and ϕ to get uniform probability in X-Y plane. Should I use r= rmax* (random(N))^0.5 or rmax(random(N))^(1./3) and ϕ=acos((2random(N)-1)? as I am interested in X-Y. In X-Y plane, It is an ellipse or circle( I interested only in X-Y) and a cone in X-Z plane. (2D BOX means 2D mesh sorry for that) – user87267 Jul 23 '13 at 00:13
-
To get the same distribution as in the second animation below, you should use $$ \begin{align} r&=r_{\text{max}}\mathrm{random}(N)^{1/3}\ \theta&=\sin^{-1}(2\mathrm{random}(N)-1)\ \phi&=\phi_{\text{min}}+(\phi_{\text{max}}-\phi_{\text{min}})\mathrm{random}(N) \end{align} $$ – robjohn Jul 23 '13 at 07:49
-
but then θ will vary only -90 to 90 ? and if I want to see the probability in X-Y plane at Z=0 they are not equal. For that I should take r=rmax*sqrt(random(N)). Remember i mainly interested in X-Y. Thank u. – user87267 Jul 23 '13 at 12:35
2 Answers
Suppose a random variable $X$ has the Cumulative Distribution Function $\Phi(t)=P(X\le t)$:
$\hspace{3.2cm}$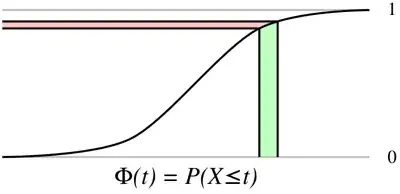
The probability of $X$ being within the base of the green region, is the height of the red region. Thus, $\Phi(X)$ is uniformly distributed along the vertical axis, $[0,1]$. Therefore, $\Phi^{-1}(U)$ has the same distribution as $X$ where $U$ is uniformly distributed in $[0,1]$.
As long as the region is radial, the CDF of being within $t$ of the origin is $$ \Phi(t)=\frac{t^3}{r^3} $$ Thus, we get the proper distribution of the distance from the origin with $$ r\,u^{1/3}\tag{1} $$ where $u$ is uniform in $[0,1]$.
Below, we look at shapes that are radially symmetric, and we need to use the signed radius $$ r\,(2u-1)^{1/3}\tag{2} $$
As shown in this answer, the the Lambert cylindrical projection preserves area. Thus. to generate a uniformly distributed point on the surface of the sphere, we can choose $z$ to be uniformly distributed in whatever range we wish, and choose $x$ and $y$ uniformly around the (possibly partial) circle.
If the region is supposed to look like this between polar angles $\phi_{\text{min}}$ and $\phi_{\text{max}}$:
$\hspace{3.2cm}$
Then we would take $$ \begin{align} z&=\cos(\phi_{\text{max}})+(\cos(\phi_{\text{min}})-\cos(\phi_{\text{max}}))v\\ y&=\sin(2\pi w)\sqrt{1-z^2}\\ x&=\cos(2\pi w)\sqrt{1-z^2} \end{align}\tag{3} $$ where $v$ and $w$ are uniform in $[0,1]$.
To get the points in the sphere, multiply the points on the sphere from $(3)$ by the radius from $(2)$.
If the region is supposed to look like this between equatorial angles $\phi_{\text{min}}$ and $\phi_{\text{max}}$:
$\hspace{3.2cm}$
Then we would take $$ \begin{align} z&=2v-1\\ y&=\sin(\phi_{\text{min}}+(\phi_{\text{max}}-\phi_{\text{min}})w)\sqrt{1-z^2}\\ x&=\cos(\phi_{\text{min}}+(\phi_{\text{max}}-\phi_{\text{min}})w)\sqrt{1-z^2} \end{align}\tag{4} $$ where $v$ and $w$ are uniform in $[0,1]$.
To get the points in the sphere, multiply the points on the sphere from $(4)$ by the radius from $(2)$.
As verified by the author, the situation is supposed to be as generated by $(4)$. Using the coordinates given in the question, we get $$ \begin{align} r&=r_{\text{max}}(2u-1)^{1/3}\\ \theta&=\sin^{-1}(2v-1)\\ \phi&=\phi_{\text{min}}+(\phi_{\text{max}}-\phi_{\text{min}})w \end{align}\tag{5} $$ where $u,v,w$ are uniform in $[0,1]$. If you don't like negative $r$, when $r\lt0$, use $$ \begin{align} r'&=-r\\ \theta'&=\theta+\pi\\ \phi'&=\phi \end{align}\tag{6} $$
10000 Points: Generated using $(2)$ and $(3)$ (top is approaching; bottom is receding)
$\hspace{3.5cm}$
10000 Points: Generated using $(2)$ and $(4)$ (top is approaching; bottom is receding)
$\hspace{3.5cm}$
-
-
It is easy to forget which way the thing is rotating and then it pulsates. I tried rotating both ways, and it is just as easy to get lost the other way, too. – robjohn Jul 22 '13 at 23:37
-
Yes.. exactly the lower plot and using the equation I mentioned also... thanks...but the your θ is not correct. – user87267 Jul 23 '13 at 16:59
-
@user87267: I actually used your equations and $(5)$ and got the same distribution as above. Why do you say that it is wrong? – robjohn Jul 23 '13 at 17:04
-
because I am getting half of the plot as in your r,θ,ϕ coordinate you wrote θ=sin−1(2v−1) which is going to -pi/2 to pi/2 but it should go between -pi to pi( or 0 to 2pi). I just want to know correct r, θ, ϕ. and also if you show the number of point in XY plane. They are not equally distributed but if r=rmax*sqrt(random(N)) then in XY (Z=0)plane number points (which shows a circle) are equally distributed. – user87267 Jul 23 '13 at 21:08
-
@user87267: That is why $r=r_{\text{max}}(2u-1)^{1/3}$ ranges over $[-r_{\text{max}},r_{\text{max}}]$; so that we get the other half filled in. Unfortunately, $\sin^{-1}(x)$ only has a range of half a full circle. Effectively, my formulas generate angles between $\frac\pi2$ and $\frac{3\pi}{2}$ when $2u-1\lt0$. – robjohn Jul 23 '13 at 21:37
-
@robjohn: Sorry for late. I was out of station. I forget to mention that I can not use r negative. Bec I have to use a function later which is velocity V=1/sqrt(r) *sin(θ)sin(ϕ). and velocity will go [-Vmax, Vmax]. So r can not be negative in my case instead I have to take θ such that[0, 2pi] it makes V in that range[-Vmax, Vmax]. Is there another way. Thanks for your response. – user87267 Jul 29 '13 at 09:34
-
@user87267: if $r\lt0$, negate $r$ and add $\pi$ to $\theta$. Essentially, I suggested this at the end of my last comment: "Effectively, my formulas generate angles between $\frac\pi2$ and $\frac{3\pi}{2}$ when $2u-1\lt0$." – robjohn Jul 29 '13 at 10:48
-
@robjohn: Are you taking absolute values of r because r will be imaginary when 2u-1<0. [because of (2u-1)^(1/3)] – user87267 Jul 29 '13 at 15:32
-
@user87267: There are three branches. Take the real one: $(-1)^{1/3}=-1$. Surely, you have seen the graph of the cube root function for the whole real line. – robjohn Jul 29 '13 at 16:38
If you want your coordinates uniform over a sphere with radius $R$, you want the density of $r$ to be proportional to $r^2$. Section 7.2 of Numerical Recipes describes how to transform uniform deviates on $[0,1]$ to a desired distribution when you can integrate the inverse function. here you want $p(y)dy=r^2\ dy$, so need to find a function $y(x)$ such that $\left | \frac {dx}{dy} \right |=y^2$, which we can see to be $x=\frac 13y^3, y=\sqrt[3]{3x}$ so your $r$ coordinate is $R\sqrt[3]{x}$ for $x$ a standard random. $\phi$ is easy-you want it uniform on $[0,2\pi]$ so just multiply a random by $2\pi$. For $\theta$, you want the density proportional to $\sin \theta$, so you need $\left | \frac {dx}{dy} \right |=\sin y$, then $x=\cos y$ and your relation is $y=\arccos (2x-1)$
- 374,822
-
if I do not want a full sphere then according to your example should I do: θ= θmin +( θmax-θmin)*(arccos(2x-1))/pi ? – user87267 Jul 22 '13 at 14:53
-
No, that would give you zero density at $\theta_{min}$ and $\theta_{max}$. The easiest is to follow the above, reject any points outside your range in $\theta$ and try again. If the allowable range in $\theta$ is not too small, this will be reasonably efficient. – Ross Millikan Jul 22 '13 at 16:31
-
After few weeks I am back in the same prob. Now my question is if θmin=-40 degree(say) and θmax=140 (say) then how could I tackle this problem as in your example θ =[0:180] which is for full sphere. My problem is still exist..I have to take different θmin and θmax which can go from -180 and 180 degree resp. You can say how θ can be from (-180 to 180). There are many different things involve so you can say it's my model. Thank you very much. – user87267 Aug 13 '13 at 22:01
-
The simplest approach is just to throw away any points outside your range in $\theta$. This is not nearly as stupid as it sounds-it is easy for your processing of the points to take $1000$ times as long as generating a random number, so even if the range gets so small you only use one in a hundred the overhead is small. This is the only choice when you can't integrate the inverse function and the reference I gave has a good discussion of the rejection method and how to make it more efficient. – Ross Millikan Aug 14 '13 at 03:29
-
I think my point was not clear. If arccos(2x−1) generates angle between(0 to 180) and I want my θmin=-40 degree and θmax=140 and I apply rejection rule then it will not consider the -40 to 0 degree. Because to reject I have to generate the point first. arccos(2x−1) only generates (0 to 180). It do not generates (-180 to 180) so if θmin=-40 degree or -20 it does not have any impact as I am generating only (0 to 180)[ y=arccos(2x−1)] – user87267 Aug 14 '13 at 09:47
-
What is $\theta=-40^\circ?$ Normally $\theta$ runs from $0$ to $180^\circ$ and $\arccos (2x-1)$ covers that range. I missed the minus sign in your original comment. – Ross Millikan Aug 14 '13 at 13:08
-
If you see my original question ϕ=ϕmin+(ϕmax−ϕmin)random(N). What I did not mention before is that I have defined ϕmin=i-w and ϕmax=i+w. Suppose, I have i=30 degree and w=90 degree. So ϕmin=-60 and ϕmax=120 degree and ϕ should be from -60 to 180. So for this case how I should apply rejection method. Remember, my i and w can be any value between 0 to 180 degree. I guess now it's clear. – user87267 Aug 14 '13 at 18:25
-
To apply rejection, you just generate a point and see if it is within range. So if $-60 \le \phi \le 180$, you reject any points where $180 \lt \phi \lt 300$. If you have an allowable range of $\theta$ you check that as well. – Ross Millikan Aug 14 '13 at 19:13
-
I did not get your last point. θ is the azimuthal angle. For my case also θ=2π[random(N)]. I am only interested in the polar angle range. If I use ϕ=arccos[2(random(N)−1)], then how I will generate negative ϕ?? As I told you I am interested on the points which is −60≤ϕ≤180 in range. What should be the form of ϕ?? – user87267 Aug 14 '13 at 23:14
-