I wanted to know how can i prove that if
$xy+yz+zx=1$, then
$$ \frac{x}{1+x^2}+\frac{y}{1+y^2}+\frac{z}{1+z^2} = \frac{2}{\sqrt{(1+x^2)(1+y^2)(1+z^2)}}$$
I did let $x=\tan A$, $y=\tan B$, $z=\tan C$
given $xy+yz+zx =1$ we have $\tan A \tan B+ \tan B \tan C+\tan C \tan A=1$
$\tan C(\tan A+\tan B)=1-\tan A \tan B$, or $\tan(A+B)=\tan(\pi/2 -C)$ we have $A+B+C=\pi/2$.
what to do now?
Any help appreciated.
thanks.
HINT:
$$\frac x{1+x^2}=\frac {\tan A}{1+\tan^2A}=\frac{2\sin A\cos A}2=\frac{\sin2A}2$$
Now , $$\sin2A+\sin2B+\sin2C=2\sin(A+B)\cos(A-B)+2\sin C\cos C$$
$$=2\sin\left(\frac\pi2-C\right)\cos(A-B)+2\sin C\cos C$$
$$=2\cos C\{\cos(A-B)+\cos(A+B)\}$$ as $\sin C=\sin\{\frac\pi2-(A+B)\}=\cos(A+B)$
$$\implies \sin2A+\sin2B+\sin2C=2\cos C\cdot2\cos A\cos B$$
and $$\frac1{\sqrt{1+x^2}}=\frac1{\sec A}=\cos A$$
The accepted answer by `lab bhattacharjee' is perfectly fine. For what it's worth, there's a nice geometric view that might enrich this nearly-4-year-old post a tiny bit.
The identity to be proven is, given $\alpha + \beta + \gamma = \frac{\pi}2$, $$ \frac12 \big( \sin 2\alpha + \sin 2\beta + \sin 2\gamma \big) = 2 \cos\alpha \cdot \cos\beta \cdot\cos\gamma$$
Consider an acute triangle $\triangle MNP$ as shown in the figure, with its circumcenter denoted as point $O$. Without loss of generality, take the circumcircle as the unit circle. That is, $$\text{diameter}~~ \overline{PP'} = 2 \qquad \text{radius}~~ \overline{OM} = \overline{ON} = \overline{OP} = 1$$
By definition, all angles are acute so that any one of them can be split into two parts, say, $\angle PMN = \alpha + \beta < \frac{\pi}2$, with a remaining complement $\gamma > 0$, as in $$\alpha + \beta + \gamma = \frac{\pi}2$$
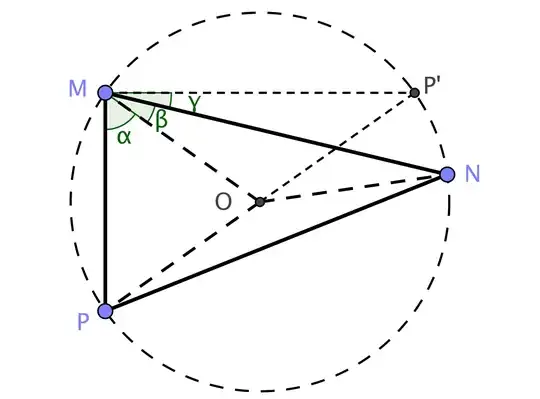
The desired identity comes from calculating the area $\mathcal{A} \equiv |\triangle MNP|$ in two different ways:
$$\begin{align} &\text{RHS}: & \mathcal{A} &= \frac12 \cdot \overline{MP} \cdot \overline{MN} \cdot \sin(\angle PMN ) \\ &\text{LHS}: & \mathcal{A} &= |\triangle OMP| + |\triangle ONM| +|\triangle OPN| \end{align}$$
For the RHS, we have $$\overline{MP} = 2\cos\alpha \qquad \overline{MN} = 2\cos\beta$$ since point $O$ is the circumcenter (e.g. $\overline{MO} = 1$ and $\triangle MOP$ is an isosceles, $\overline{MP}$ is bisected by the height to point $O$). That is, $$\begin{align} &\text{RHS}: & \mathcal{A} &= \frac12 \cdot \overline{MP} \cdot \overline{MN} \cdot \sin(\angle PMN ) \\ && &= \frac12 \cdot 2\cos\alpha \cdot 2\cos\beta \cdot \sin(\alpha + \beta) \\ && &= 2\cos\alpha \cdot \cos\beta \cdot \sin(\frac{\pi}2 - \gamma) \\ && &= 2\cos\alpha \cdot \cos\beta \cdot\cos\gamma \end{align}$$
Now, for the LHS we again apply the Law of Sines to each of the small triangles. For example, $$\begin{align} \triangle{NOP} &= \frac12 \cdot \overline{ON} \cdot \overline{OP} \cdot \sin(\angle NOP) \\ &= \frac12 \cdot 1 \cdot 1 \cdot \sin(\pi - \angle NOP') \\ &= \frac12 \sin(\pi - 2\gamma) \end{align}$$ since $\angle NOP'$ is the central angle for the inscribed angle $\gamma$ (and $\triangle PMN$ is acute so $O$ is "inside"). Therefore, we have $$\triangle{NOP} = \frac12 \sin 2\gamma \qquad \text{and similarly} \qquad \triangle{POM} = \frac12 \sin 2\alpha \quad \triangle{MON} = \frac12 \sin 2\beta$$ which sum to the LHS of the desired identity. Note how this proof (splitting a triangle into 3 inner ones) naturally exhibits the cyclic nature (3-fold symmetry) of the identity. $~~~~~$Q.E.D.
When the triangle is obtuse, the proof is similar: one of $\alpha, \beta, \gamma$ is negative, which corresponding 'inner' triangle becomes `outer', and its effective area is also negative). For the case where two of $\alpha, \beta, \gamma$ are negative, unfortunately the notion of a triangle breaks down (unless one considers projective geometry, I guess).
P.S.
I definitely have seen this triangle-splitting analysis before at various places, with respect to any general point and not just the circumcenter. The corresponding algebraic expression involves more than 3 angles.
