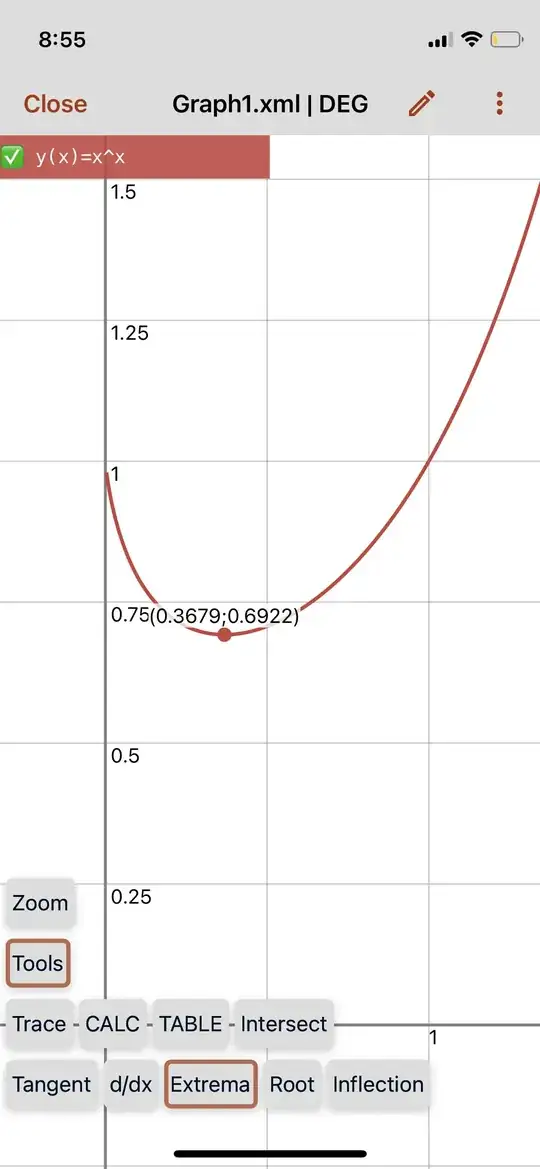
Does there exist an application that makes use of the degenerate case of $x^x$ in the unit range?
For most of the function $x^x$ the y value's progression as $x$ increases or decreases makes sense. But within the unit range (specifically at the extrema 0.3679...) something non-intuitive occurs. I find this inherently interesting but I've been challenged to provide an application for the phenomenon.
Are there any?