How to prove that $\lim\limits_{x\to0}\frac{\tan x}x=1$?

Question

How to prove that $$\lim\limits_{x\to0}\frac{\tan x}x=1?$$

I'm looking for a method besides L'Hospital's rule.

Answer 1

Strong hint: $$\displaystyle \lim \limits_{x\to 0}\left(\frac{\tan (x)}{x}\right)=\lim \limits_{x\to 0}\left(\frac{\tan (x)-0}{x-0}\right)=\lim \limits_{x\to 0}\left(\frac{\tan(x)-\tan(0)}{x-0}\right)=\cdots$$

Answer 2

Consider the unit circle with center $O$. Let $A$ be a fixed point on the circumference. Let $X$ be a point on the circumference such that $\angle AOX = x$.

Let the tangent at $X$ intersect $OA$ extended at $B$. Since $\angle OXB = 90^\circ$ hence $BX = \tan x$.

Then, the area of the sector $OAX$ is $\frac{x\times 1^2}{2}$ and the area of the triangle $OXB$ is $\frac{1 \times \tan x}{2}$. It is clear that as $X$ tends towards $A$, the limit of these areas is $1$.

Answer 3

$$\tan { x } =x+\frac { { x }^{ 3 } }{ 3 } +\frac { 2{ x }^{ 5 } }{ 15 } +\cdots \\ \frac { \tan { x } }{ x } =\frac { x+\frac { { x }^{ 3 } }{ 3 } +\frac { 2{ x }^{ 5 } }{ 15 } +\cdots }{ x } =1+\frac { { x }^{ 2 } }{ 3 } +\frac { 2{ x }^{ 4 } }{ 15 } +\cdots \\ \lim _{ x\rightarrow 0 }{ \left( \frac { \tan { x } }{ x } \right) } =1$$Or for the geometric proof see:http://www.proofwiki.org/wiki/Limit_of_Sine_of_X_over_X/Geometric_Proof

Answer 4

In order to find the derivative of $\sin x$, many calculus courses start by proving, sort of, that $$\lim \limits_{x\to 0}\frac{\sin x}{x}=1.\tag{1}$$

If that is already taken as "known" in your course, note that unless $\cos x=0$, we have
$$\frac{\tan x}{x}=\frac{1}{\cos x}\frac{\sin x}{x}.$$ Now we can take the limit. Use (1) and the fact that $\cos x$ is continuous at $0$ and therefore $\lim \limits_{x\to 0}\cos x=1$.

Answer 5

Consider the following circle with a regular $n$ side polygon inside:

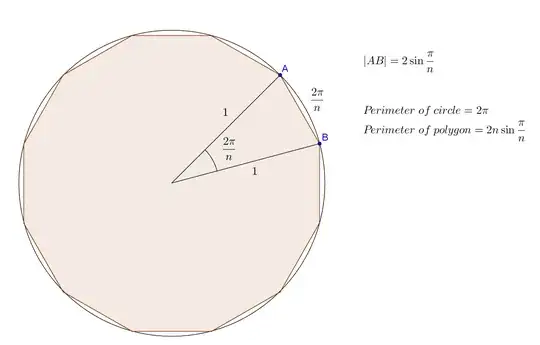
We know that if the polygon have more sides the its perimeter will get closer to the perimeter of circle. $$\lim _{ n\rightarrow \infty }{ \frac { Perimeter\ of\ polygon }{ Perimeter\ of\ circle } } =\lim _{ n\rightarrow \infty }{ \frac { 2n\sin { \frac { \pi }{ n } } }{ 2\pi } } =\lim _{ n\rightarrow \infty }{ \frac { \sin { \frac { \pi }{ n } } }{ \frac { \pi }{ n } } }=1. $$ Assume $x=\frac { \pi }{ n } $ then we get $$\lim _{ x\rightarrow 0 }{ \frac { \sin { x } }{ x } } =1.$$We already know $\lim _{ x\rightarrow 0 }{ \cos x } =1$, therefore $$\lim _{ x\rightarrow 0 }{ \frac { \tan { x } }{ x } } =1.$$

Answer 6

You could expand $tan(x)$ as a power series and then divide all terms by $x$ and then take the limit?

Answer 7

Here's mine!

$$\lim_{x \to 0} \frac{\tan x}{x}$$ $$= \lim_{x \to 0} \sec x\frac{\sin x}{x}$$ $$= \bigg(\lim_{x \to 0}\sec x\bigg) * \bigg(\lim_{x \to 0} \frac{\sin x}{x}\bigg)$$ $$= \bigg(\lim_{x \to 0}\cos x\bigg)^{-1} * 1 $$ $$= 1^{-1} * 1$$ $$= 1$$ :)

Answer 8

This limit is proven in this answer. That answer was in response to the question of how to show $$ \lim_{x\to0}\frac{\sin(x)}{x}=1 $$ However, since $\cos(x)$ is continuous at $x=0$, the two questions are related: $$ \begin{align} \lim_{x\to0}\frac{\tan(x)}{x} &=\lim_{x\to0}\frac1{\cos(x)}\frac{\sin(x)}{x}\\ &=\frac1{\cos(0)}\lim_{x\to0}\frac{\sin(x)}{x}\\[6pt] &=1 \end{align} $$

Answer 9

One way to look at it is to consider an angle subtended by two finite lines, both of magnitude r, where the angle between them is x (we take x to be small). If you draw this out, you can see there are "3 areas" you can consider. One is the area enclosed with a straight line joining the two end points, an arc and lastly considering a right-angled triangle. Sorry I cant provide a diagram, I'm new to maths.stackexchange :)

you get the following result

1/2*r^2sinx < 1/2*r^2x < 1/2*r^2tanx for small x, with simplication we get

sinx < x < tanx divide by tanx yeilds

cosx < x/tanx < 1 taking the limit as x goes to 0, (which we can do as we took x to be small)

we get 1 < x/tanx < 1, by squeeze theorem this tells us the limit of as x >>0 for x/tanx is 1. Now the limit of tans/x as x approaches 0 will be the reciprocal of this. I should mention I am assuming early foundational results regarding limits in an Analysis course. Hence, the limit is 1.

Answer 10

We know that if the polygon have more sides the its perimeter will get closer to the perimeter of circle. $$\frac{HB}{R}=\tan \left(\frac{360}{2n}\right)=\tan \left(\frac{π}{n}\right)\\AB=2HB=2R\tan \left(\frac{π}{n}\right)$$ Perimeter of polygon = $nAB=2nR\tan \left(\frac{π}{n}\right) \\$

Perimeter of circle = $2π R $

Now when $n → \infty $ $$ \lim_{n \to \infty } \frac{\text{Perimeter of polygon}}{\text{Perimeter of circle}}=1$$ $$\lim_{n → \infty } \frac{2n R \tan \left(\frac{π}{n}\right)}{2 π R }=1$$ $$\lim_{n → \infty } \frac{n \tan \left(\frac{π}{n}\right)}{ π }=1$$ $$\lim_{n → \infty } \frac{\tan \left(\frac{π}{n}\right)}{\frac{π}{n}}=1$$

Obviously $\frac{π}{n} → 0$ name as $x$ so $$ \lim_{n → \infty } \frac{\tan \left(\frac{π}{n}\right)}{\frac{π}{n}}=\lim_{x → 0 } \frac{\tan \left(x\right)}{x}=1$$

Answer 11

Using L'Hôpital rule, we'll see $$ \lim_{x\to\infty}\frac{\mathrm{tan}(x)}{x}=\lim_{x\to\infty}\frac{\left (\mathrm{cos}^{2}(x) \right )^{-1}}{1}=\lim_{x\to\infty} 1-\mathrm{sin}^{2}(x)=\dots $$

Answer 12

$$\lim_{x\rightarrow 0} \frac{\tan (x)}{x} = \frac{d}{dx}\tan(0)=\sec^2(0)=1$$

This, I find, is the simplest method of showing it...