How to heuristically minimize the area between a line through a fixed point and the coordinate axes.

Question

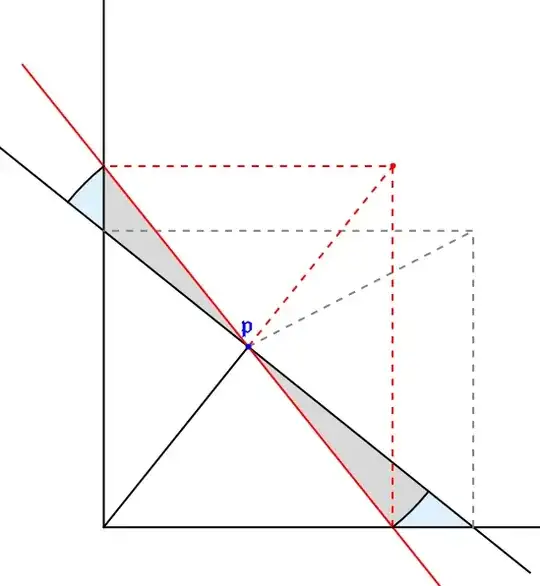
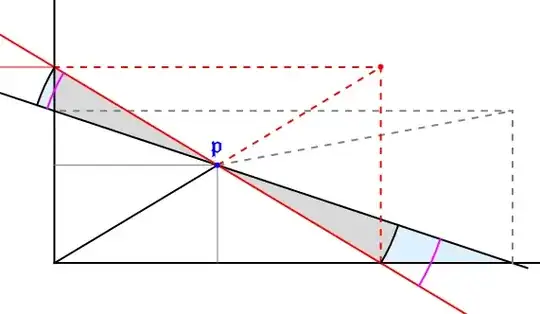
This is an exercise in Tristan Needham's Visual Differential Geometry and Forms. He uses the term ultimate equality to mean roughly the same thing as first order approximation, which he says is motivated by Newton's Principia. The book is dedicated to Needham's longtime personal friend Roger Penrose, and is worthy of the dedication.

The first part, using calculus is pretty straight forward. Divide the triangle into a rectangle of area $ab,$ an upper triangle of height $a\tan{\theta}$ and a lower triangle of base $b\cot{\theta}.$ Add the resulting areas to get $\mathcal{A}.$ Set the derivative equal to zero. Put the resulting value for $\tan\theta$ into the expression for area.

\begin{align*} \mathcal{A}= & \frac{1}{2}\left(2ab+a^{2}\tan\theta+b^{2}\cot\theta\right)\\ \mathcal{A}^{\prime}= & \frac{1}{2}\left(\frac{a^{2}}{\cos^{2}\theta}-\frac{b^{2}}{\sin^{2}\theta}\right)=0\\ \tan\theta= & \frac{b}{a}\implies\mathcal{A}=2ab \end{align*}

But I haven't figured out the "trick" intended by the second part. See the text in bold-face. The solution involves drawing a picture something like my first drawing. The "ultimate equality" expressions will be the kinds physicists write, and mathematicians say "you can't do that."

Let $L$ be a general line through the point $\left\{ a,b\right\} $ in the first quadrant of $\mathbb{R}^{2}$, and let $\mathcal{A}$ be the area of the triangle bounded by the $x$-axis, the $y$-axis and $L$.

(i) Use ordinary calculus to find the position of $L$ that minimizes $\mathcal{A}$, and show that $\mathcal{A_{\min}}=2ab.$

(ii) Use Newtonian reasoning to solve the problem instantly, without calculation! (Hints: Let $\delta\mathcal{A}$ be the change in the area resulting from a small (ultimately vanishing) rotation $\delta\theta$ of $L$. By drawing $\delta\mathcal{A}$ in the form of two triangles, and observing that each triangle is ultimately equal to a sector of a circle, write down an ultimate equality $\delta\mathcal{A}$ in terms of $\delta\theta$. Now set $\delta\theta=0.$)

The drawings represent two attempts to produce the "immediate" solution. But neither approach seems to give a simple, and obvious formulation of $\delta\mathcal{A}$ that leads directly to the equation $\mathcal{A}=2ab.$

The red line is the correct solution. The black (or green) line is the result of rotating through $\delta\theta$. I've added another image with a greater difference between $a$ and $b$ to show more clearly that the light blue triangles are not equal.

How should the approach described in the "hints" be depicted?

Answer 1

Here is how I had done it, so I take your pic:

The situation is that no matter what size rotation we take, $\langle A = \langle B$. Now the next thing to notice is that as the red line $(a,b)$ about an infinitesimal angle (clockwise) , we lose area in sector spanned by $A$ and gain area in sector spanned by $B$. In the small angle limit, the contribution of blue parts to the total area of sector is zero, so the area of the blue triangular part is roughly zero.

This lets us wrote the differential area change as,

$$ dA =\frac{ r_1^2 d \theta - r_2^2 d \theta }{2}= \frac{\left(r_1^2 - r_2^2 \right) d \theta}{2}$$

Where $r_1$ and $r_2$ is distance from $p$ to the original x and y intercepts. If we want an the configuration to be such that area is maximum, nudging the parameter should leave the differential area zero upto first order in $\theta$, this can be achieved with the following equality:

$$r_1^2 = r_2^2$$

Which leads to $r_1=r_2$. This means distance from point to x intercept= distance from point to y intercept, this can be used to show that the coordinate of the intercept are same i.e: $(a,0) = (0,a)$.

Now use equation of area of right triangle for final answer.

Answer 2

As others have pointed out. The problem amounts to showing that the fixed point is the midpoint between the intercepts along the solution line. Once that is established its a matter of trivial geometry to show $\mathcal{A}=2ab.$

The magenta circular arcs intersect the axes between the solution line and the varied line. The point of intersection is chosen to make the sector areas exactly equal to the corresponding variation triangles. The points of intersection determine the associated radii. These sector areas need to be ultimately equal in order to have a stationary value of $\theta$. Since the points of intersection along each axis converge as $\delta\theta$ goes to $0,$ the distance from $\left(a,b\right)$ to the points of intersection must become equal.

Both $\delta r_{x}$ and $\delta r_{y}$ are positive numbers. We now have:

\begin{align*} \delta\mathcal{A}= & \frac{1}{2}\left(\left(r+\delta r_{x}\right)^{2}-\left(r-\delta r_{y}\right)^{2}\right)\delta\theta\\ = & r\left(\delta r_{x}+\delta r_{y}\right)\delta\theta. \end{align*}

Needham actually introduces a standard of proof which he calls "beyond a reasonable doubt." I will have to invoke this, since the vanishing of $\delta\theta$ is sufficient for $\delta\mathcal{A}$ to vanish. Nonetheless, it is evident that $\left(\delta r_{x}+\delta r_{y}\right)$ must also vanish with $\delta\theta.$ But I can only wave my hands, and say it does.