$P(T_1 \cap T_2 | D)$ : Probability that the results are positive in both the tests given Fred has the disease.
$P(T_1 \cap T_2)$ : Probability that the results are positive in both the tests taking into account both the cases - when Fred has the disease and when not.
Does this mean that $P(T_1 \cap T_2) = P(T_1 \cap T_2 | D) P(D) + P(T_1 \cap T_2 | D^c) P(D^c)$?
Yes, yes, and yes.
A rare disease afflicts only $1\%$ of the population. Fred gets tested for it with two diagnostic tests. The sensitivity and specificity of the second test are both $0.95,$ and knowing that Fred has the disease makes the second test independent of the first.

- Is it true that $P(T_1 \cap T_2 | D) = P(T_1 | D)\times P(T_2 | D)$?
This is definitionally equivalent to the statement “events $T_1$ and $T_2$ are conditionally independent given event $D.$”
It is true here, since knowing that Fred has the disease makes the two tests independent. The computation: $$P(T_1 T_2 \mid D) = 0.95x = (0.95x +0.05x)\times0.95= P(T_1 \mid D)\times P(T_2 \mid D).$$
- Is it true that $P(T_1 \cap T_2) = P(T_1)\times P(T_2)$?
Not necessarily, even in the given scenario: $$P(T_1 T_2)
\\=(0.01)(0.95)x+(0.99)(0.05)y
\\=0.0095x+0.0495y
\\\not\equiv 0.00059x+0.0029205y+0.0554895z
\\=\Big(0.01x+(0.99)(0.05y+0.95z)\Big) \times \Big((0.01)(0.95)+(0.99)(0.05)\Big)
\\=P(T_1)\times P(T_2).$$
So, the two tests being independent conditional on Fred having the disease does not imply that the two tests are independent! ҂ †
but aren't medical tests supposed to be independent regardless of the disease status?
No, medical tests are not in general independent of each other! Knowledge of a positive result for Hepatitis B increases the probability of a positive result for HIV; ceteris paribus, the second of two successive COVID swab tests on the same subject is more probable than the first to register negative, due a lower concentration of antigens in the second reagent tube. So, for this COVID-test example, $P(T_2|T_1^\complement) < P(T_2).$
҂ More interestingly, the converse is also false: independence does not imply conditional independence (so, neither independence nor conditional independence implies the other).
In the following example, $T_1$ and $T_2$ are independent, yet, given that $D$ happens, $T_1$ and $T_2$ are dependent!
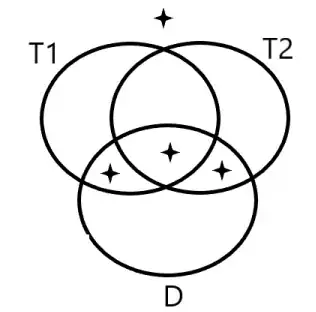
$$P(T_1T_2)=\frac14=P(T_1)\times P(T_2),$$ yet, given that $\boldsymbol D$ happens, $$P(T_1 T_2) =\frac13\ne \frac49 = P(T_1)\times P(T_2).$$
Notably, given that $\boldsymbol{D^\complement}$ happens, $$P(T_1 T_2) = 0 = P(T_1)\times P(T_2);$$ hence, $T_1$ and $T_2$ being either dependent or independent conditional on whether $D$ happens does not imply that $T_1$ and $T_2$ are dependent!!
† Remarkably, events $X$ and $Y$ being independent conditional on event $A$ as well as conditional on event $A^\complement$ still does not imply that $X$ and $Y$ are independent!!
For example, let $E$ be an event with probability strictly between $0$ and $1;$ then $$P(E\cap E\mid E)=1=P(E\mid E)\times P(E\mid E),\\
P(E\cap E\mid E^\complement)=0=P(E\mid E^\complement)\times P(E\mid E^\complement),$$ yet $$P(E\cap E)=P(E)\ne [P(E)]^2=P(E)\times P(E).$$
Alternatively, here's a less abstract, coin-toss example.

