3

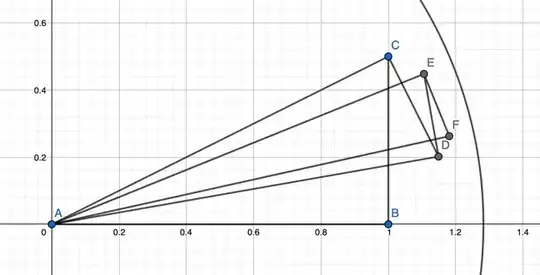
Motivated by this question I considered the alternating sum of vectors illustrated here:

enter image description here

To describe this, there is a vector $\langle1,0\rangle$ of length $1$. Then add an orthogonal vector of length $\frac12$. From, there, add an orthogonal vector of length $\frac13$. Then of length $\frac14$, and so on. The direction of the vector being added alternates between positive and negative vertical components. The image shows up to the 5th partial sum.

It is known the magnitude is converging to $\frac{\pi}{\sqrt{6}}$ by the Basel problem. The image includes a circle with that radius.

The angle is converging based on the alternating series test, but to what? The angle of the $n$th vector is $$\sum_{k=2}^{n}(-1)^{k}\arctan\left(\frac{1/k}{\sqrt{H^{(2)}_{k-1}}}\right)$$ where $H^{(2)}_n$ is the $n$th Harmonic number of degree $2$. That is, $H^{(2)}_n=1+\frac14+\frac19+\cdots+\frac{1}{n^2}$.

Can we express this angle in some closed form (not as an infinite sum)? Numerically, it converges slowly (similar to the alternating Harmonic series) to about $0.29328$.

2'5 9'2
  • 54,717

1 Answers1

3

This is not an answer but let me share your dream for a possible closed form.

$$a_k=(-1)^k \tan ^{-1}\left(\frac{1}{k \sqrt{H_{k-1}^{(2)}}}\right)$$ $$a_k+a_{k+1}=(-1)^k \tan ^{-1}\left(\frac{(k+1) \sqrt{H_k^{(2)}}-k \sqrt{H_{k-1}^{(2)}}}{1+k (k+1) \sqrt{H_{k-1}^{(2)}\, H_k^{(2)}}}\right)$$ could be interesting to exploit.

The expansion of the $\tan ^{-1}(*)$ is $$\frac{\sqrt{6}}{\pi k^2}\Bigg[1-\frac{\pi ^2-6}{\pi ^2 k}+\frac{81-21 \pi ^2+2 \pi ^4}{2 \pi ^4 k^2}-\frac{-270+99 \pi ^2-17 \pi ^4+\pi ^6}{\pi ^6 k^3}+O\left(\frac{1}{k^4}\right) \Bigg]$$ The infinite summation is a bit faster and converges to the number you gave $0.293285163191864$

Claude Leibovici
  • 260,315