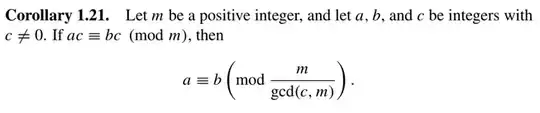Attached below is a statement and a proof from the book "104 Number Theory Problems" by Dorin Andrica, Titu Andreescu, and Zuming Feng.
Here is the corollary mentioned in the proof.
The point I'm having trouble understanding is how they declared there exist $(u,v) \geq0$ such that $\gcd(x,y)=ux-vy$. From my understanding of Bezout's identity, there exist countably infinite integer solutions to $ax+by=\gcd(x,y)$, but how exactly is a positive-negative pair guaranteed? For positive integers $(x,y)$, I understand why this has to true as their gcd has to be less than or equal to both of them, hence one of the coefficients needs to be negative. When $(x,y)$ are both negative, it's possible to just flip the signs of the solution pair of $a(-x)+b(-y)=\gcd(-x,-y)$ as $\gcd(x,y)=\gcd(-x,-y)$. The cases where either $x$ or $y$ is negative are the ones I can't seem to justify.
On another note, why was this declaration required? The proof remains valid using integers $(a,b)$ as in $ax+by$ instead of $ux-vy$.
Any help is appreciated.