6

Given the known theorems $P \Rightarrow Q$ and $\lnot P$, prove that we cannot deduce $\lnot Q.$

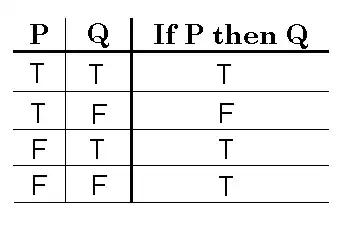
I made the truth table for $P \Rightarrow Q:$

if p then q

Now, if $P \Rightarrow Q$ is a theorem, that means that we must exclude the second row of the truth table.

If $\lnot P$ is also a theorem, that means that $\lnot P$ is true, so $P$ must be false. Therefore, we must look in the last 2 rows of the truth table, since they're the only ones where $\lnot P$ and $P \Rightarrow Q$ are true at the same time.

I don't understand why we can't deduce $\lnot Q$ from $P \Rightarrow Q$ and $\lnot P.$ After all, if we are looking in the fourth row of the truth table where $P \Rightarrow Q$ is true and $\lnot P$ is true, then$\lnot Q$ is also true.

ryang
  • 38,879
  • 14
  • 81
  • 179
David
  • 224
  • 1
  • 7
  • 7
    Doesn't your third row provide the counter-example? – John Douma Jun 19 '22 at 15:23
  • 1
    +1 to your question. Nicely presented and reasoned, with good work shown. As you reasoned, the combined premises of [1] $P \implies Q$ and [2] $\neg P$ indicate that only rows three and four are pertinent. For the assertion to hold, the conclusion that $Q$ is always false would have to hold for both of the pertinent rows. As the comment of John Douma indicates, row three is therefore a counter-example to the assertion. – user2661923 Jun 19 '22 at 15:51
  • If Spot is a dog, then Spot is a mammal. Spot is not a dog. – paw88789 Jun 20 '22 at 13:54
  • What if $P$ is $Q\land \neg Q?$ Then $\neg P$ is $(\neg Q)\lor Q$..... or 2. If I am asleep then I am not-invisible. Does it follow that if I am awake then I am invisible? .... or 3 . $P\implies Q$ is $\mathbf {defined} $ as $(\neg P)\lor Q.$
    • – DanielWainfleet Jun 20 '22 at 15:25