How to prove the inequality including Bessel functions?

Question

As well-known the modified Bessel functions of orders zero and one of the first kind, $I_0(x)$ and $I_1(x)$ are positive and increasing functions over $x\in(0, \infty)$, while the modified Bessel functions of orders zero and one of the second kind, $K_0(x)$ and $K_1(x)$ are positive and decreasing functions over $x\in(0, \infty)$.

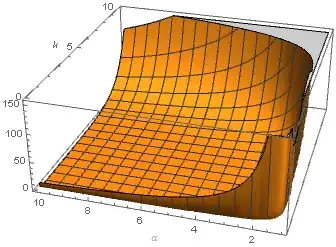
How can I prove the following inequality with $\alpha>1$ and $k>0$?

$$I_0(k\alpha)K_1[k(\alpha-1)]-K_0(k\alpha)I_1[k(\alpha-1)]>0.$$

In other words, how to prove $I_0(x)K_1(y)>K_0(x)I_1(y)$ with $x>y>0$?

I believe the inequality is true as can be observed by plotting. Thank you very much!

Answer 1

Introduce the function $$ f(x,t)=I_0(x+t)K_1(x)-K_0(x+t)I_1(x). $$ We want to show that $f(x,t)>0$ for all $x>0,t\geq 0$.

Consider first the case $f(x,0)$. We can prove that $f(x,0)>0$ by writing $$ f(x,0)=(I_0(x)-I_1(x))K_1(x)+I_1(x)(K_1(x)-K_0(x)) $$ and using the monotonicity properties (see here: https://dlmf.nist.gov/10.37) $$ I_0(x)>I_1(x)\mbox{ and }K_1(x)>K_0(x)\mbox{ for all }x>0. $$

Next, by a direct computation, we have $$ \frac{\partial}{\partial t}f(x,t) =I_1( t + x) K_1(x) + I_1(x)K_1(t + x) $$ which is manifestly positive for $x>0,t\geq 0$. Hence $$ f(x,t)=f(x,0)+\int_0^t (I_1( \tau+ x) K_1(x) + I_1(x)K_1(\tau + x))\mathrm d \tau>0. $$

Answer 2

In other words, you want to prove that, for the worst case, $$f(x)=I_0(x)\, K_1(x)-I_1(x)\, K_0(x)~>~0$$

It is simple if you consider small and large values of $x$.

Using their asymptotic values,

$$f(x)=\frac{1}{x}+O\left(x\right)$$ $$f(x)=\frac{1}{2 x^2}+O\left(\frac{1}{x^4}\right)$$

If you want to go further, use Hankel's asymptotic values which will give $$f(x) = \frac{1}{2 x^2}+\frac{3}{16 x^4}-\frac{45}{32768 x^6}+\cdots$$ which is extremely good as soon as $x>\frac 32$.