Area of a square inscribed in a square

Question

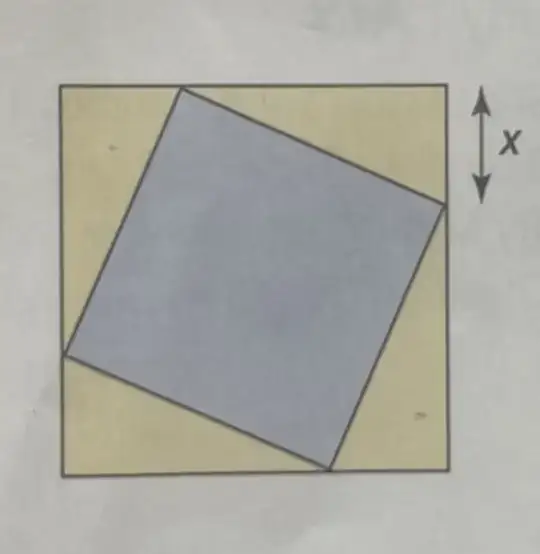
I was doing a mathematics question from my textbook and the question says to express the area of the inscribed square as a function of $x$. We are also given that the length of the large square is $10$ units. My reasoning was to first see that the area of the large square is $10 \times 10 = 100$ sq units. Then I called the height of the right triangles along the outside of the inscribed squares as $h$. After this, I got the area of all the triangles, multiplied it by $4$, and then subtracted it from $100$. To get the final expression of $100-2xh = f(x)$. Does anyone know what I did wrong? Any help would be greatly appreciated.

I understand that getting the side lengths and then squaring it will get the answer. But why doesn't the way I did it work? Intuitively it should, right? — Jaireet Chahal, Jun 16 '22 at 19:32

score 6 · Accepted Answer · answered Jun 16 '22 at 19:34

There's nothing wrong, but you haven't finished yet. Just note $h=10-x$, so the area of the inscribed square in terms of $x$ is $$f(x)=100-2x(10-x)=100-20x+2x^2.$$

This aside, you can compute $f(x)$ even easier just using the Pythagorean Theorem: $$f(x)=h^2+x^2=(10-x)^2+x^2=100-20x+2x^2.$$

Area of a square inscribed in a square

1 Answers1