The following is a problem from chapter 13, "Integrals", from Spivak's Calculus
- Suppose that $f$ is a continuous increasing function with $f(0)=0$. Prove that for $a,b>0$ we have Young's Inequality,
$$ab\leq \int_0^a f(x)dx+\int_0^b f^{-1}(x)dx\tag{1}$$
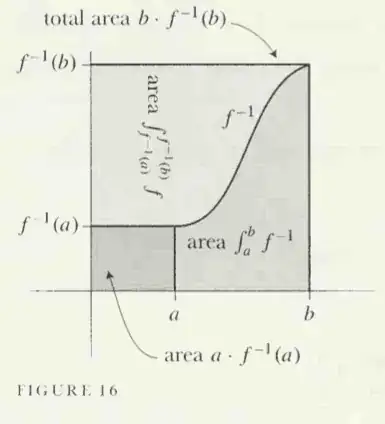
and that equality holds if and only if $b=f(a)$. Hint: Draw a picture like Figure 16.
The cited picture 16 isn't that important, it is just an example
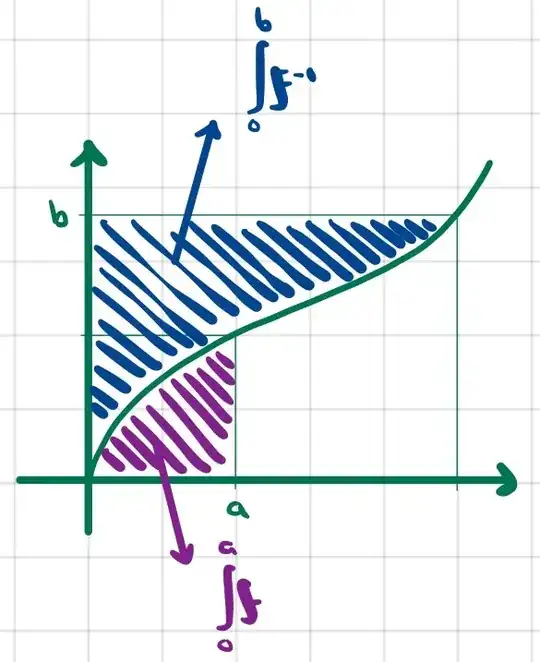
When one draws a picture, $(1)$ is intuitively pretty obvious
Above is the case where $b>f(a)$.
I spent a while thinking about how to prove $(1)$ analytically. Finally, I looked at the solution manual and the solution there was just the obvious intuitive solution I had first thought of, but without the equations I spent time trying to find. Here it is
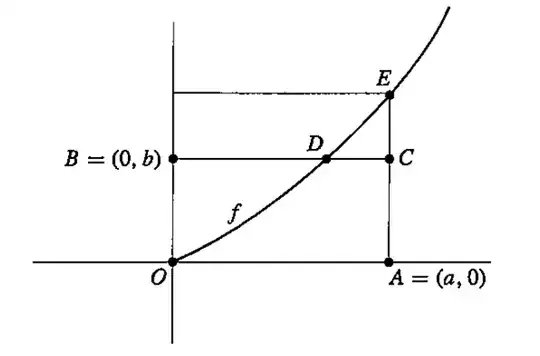
The figure below shows the case $b<f(a)$.
We have $$ab=\text{ area } OACB<\text{ area } OAE+ \text{ area } OBD$$ $$=\int_0^a f(x)dx+\int_0^bf^{-1}(x)dx$$
If $b=f(a)$ we clearly have equality. It is easy to see that we have the same inequality if $b>f(a)$ (or simply apply the first inequality to $f^{-1}$).
Is this proof considered rigorous? Is there one that uses equations instead of words like "clearly".